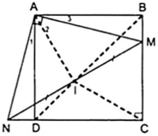
Áp dụng định nghĩa và giả thiết của hình vuông ABCD ta được:
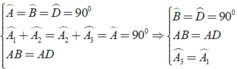
⇒ Δ ABM = Δ ADN( g - c - g )
Do đó AM = AN (cặp cạnh tương ứng bằng nhau)

Áp dụng định nghĩa và giả thiết của hình vuông ABCD ta được:
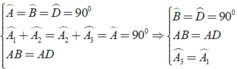
⇒ Δ ABM = Δ ADN( g - c - g )
Do đó AM = AN (cặp cạnh tương ứng bằng nhau)
Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, qua A kẻ AN ⊥ AM (điểm N thuộc tia đối của tia DC). Gọi I là trung điểm của MN. Chứng minh rằng: Ba điểm B, I, D thẳng hàng.
Mọi Người giúp em chi tiết với ạ
Cho hình vuông ABCD cạnh a. Lấy điểm M bất kì trên BC. Trên tia đối của tia DC lấy điểm N sao cho DN=BM.
a ) Chứng minh AN=AM.
b ) Kẻ AI MN tại I, tia AI cắt DC tại F. Lấy E đối xứng với F qua I. Chứng minh NEMF là hình thoi
c ) Đường vuông góc với AM tại M cắt đường vuông góc với AN tại N ở H. Chứng minh : AN= AM và ba điểm A, I, H thẳng hàng.
d ) Chứng minh rằng khi M thay đổi vị trí trên BC thì chu vi tam giác MFC luôn không đổi.
Cho hình vuông ABCD. Trên cạnh AB lấy điểm M, trên tia đối của CB lấy điểm N sao cho AM =CN . Gọi Ilà giao điểm của MN và CD.
GọI E là trung điểm của MN, tia DE cắt BC tại F. Qua M vẽ đường thẳng song song với AD cắt DF tại H.
Chứng minh rằng : Tứ giác MFNH là hình thoi.
Chứng minh : Chu vi tam giác BMF không đổi khi m di động trên cạnh AB.
Cho hình vuông ABCD, M là một điểm nằm giữa B và C. Kẻ AN vuông góc với AM, AP vuông góc với MN ( N và P thuộc đường thẳng CD)
1. Tính tỉ số chu vi tam giác CMP và chu vi hình vuông ABCD
2. Gọi Q là giao điểm của tia AM và tia DC. Chứng minh tổng 1/AM2 +1/AQ2 không đổi khi điểm M thay đổi trên cạnh BC.
Cho hình vuông ABCD. E là điểm trên cạnh DC, F là điểm trên tia đối của tia BC sao cho BF = DE.
a) Chứng minh tam giác AEF vuông cân.
b) Gọi I là trung điểm của EF. Chứng minh I thuộc BD.
c) Lấy điểm K đối xứng với A qua I. Chứng minh tứ giác AEKF là hình vuông
Hình vuông ABCD cạnh bằng a. Trên BC lấy điểm M, trên tia đối của tia DC lấy điểm N sao cho BM=DN. Vẽ AH vuông với NM (H thuộc NM), AH cắt DC ở E. Gọi G là giao điểm của MN với AD.
a/ CM tam giac NAM vuông cân và D,H,B thẳng hàng
b/ Tính chu vi tam giác EMC theo a.
c/ Gọi I là giao điểm của BD với AM. Gọi K là giao của EG với AN. CM AIEK là hình vuông
Cho hình vuông ABCD, E là điểm trên cạnh DC, F là điểm trên tia đối của tia BC sao cho BF = DE.
a) Chứng minh tam giác AEF vuông cân.
b) Gọi I là trung điểm của EF .Chứng minh I thuộc BD.
c) Lấy điểm K đối xứng với A qua I.Chứng minh tứ giác AEKF là hình vuông.
Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của Am ; d là điểm đối xứng với M qua I. a) Chứng minh tứ giác AMCd là hình chữ nhật.b trên tia am lấy điểm m sao cho ma= mn . từ i kẻ ih vuông góc với mc (h thuộc mc ) chứng minh điểm d đối xướng với điểm n qua h
Cho hình vuông ABCD có cạnh bằng a. Trên BC lấy M, trên tia đối của tia DC lấy N sao cho BM = DN. Vẽ AH vuông góc với NM ( H thuộc NM), AH cắt DC tại E. Gọi G là giao điểm của MN với AD
a, CMR tam giác NAM vuông cân bà D, H, B thẳng hàng
b, Tính chu vi tam giác EMC theo a
c, Gọi I là giao điểm của BD với AM, gọi K là giao điểm của EG với AN. CMR: tứ giác AIEK là hình vuông