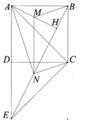
Cho hình vuông ABCD. Gọi E là điểm đối xứng của điểm A qua điểm D.
a) Chứng minh tam giác ACE là tam giác vuông cân.
b) Từ A hạ AH ^ BE, gọi M và N theo thứ tự là trung điểm của AH và HE. Chứng minh tứ giác BMNC là hình bình hành.
c) Chứng minh M là trực tâm của tam giác ANB.
d) Chứng minh A N C ^ = 90 0 .
a) E là điểm đối xứng của điểm A qua điểm D Þ A, D, E thẳng hàng và DA = DE Þ CD ^ AE tại trung điểm của AE Þ CA = CE Þ DCAE cân ở C.
Þ D A C ^ = 450 Þ DACE vuông cân.
b) Áp dụng tính chất đường trung bình cho DHAE và giả thiết ABCD là hình vuông ta sẽ chứng minh được tứ giác BMNC là hình bình hành.
c) Do AH ^ BN, mà NM//CB Þ NM ^ AB nên M là trực tâm của tam giác ANB.
d) M là trực tâm DABN nên BM ^ AN mà BM//CN Þ A N C ^ = 900