S ABCD=36cm2
=>\(AB=\sqrt{36}=6\left(cm\right)\)
\(AC=\sqrt{6^2+6^2}=6\sqrt{2}\left(cm\right)\)
=>\(R=\dfrac{6\sqrt{2}}{2}=3\sqrt{2}\left(cm\right)\)
\(S=R^2\cdot3.14=18\cdot3.14=56.52\left(cm^2\right)\)
S ABCD=36cm2
=>\(AB=\sqrt{36}=6\left(cm\right)\)
\(AC=\sqrt{6^2+6^2}=6\sqrt{2}\left(cm\right)\)
=>\(R=\dfrac{6\sqrt{2}}{2}=3\sqrt{2}\left(cm\right)\)
\(S=R^2\cdot3.14=18\cdot3.14=56.52\left(cm^2\right)\)
Tính chu vi của đường tròn ngoại tiếp và diện tích của hình tròn nội tiếp hình vuông có cạnh 20 cm
Cho hình thang vuông ABCD (AB là đáy nhỏ) biết góc C bằng 60 độ, AB bằng 6 cm, BC = 10 cm. Tính chu vi và diện tích hình thang ABCD.
Cho hình vuông ABCD cạnh y (cm). Điểm E thuộc cạnh AB. Điểm G thuộc tia AD sao cho AG = AD + (3/2)EB. Dựng hình chữ nhật GAEF. Đặt EB = 2x (cm).
Tính x và y để diện tích hình chữ nhật bằng diện tích hình vuông và ngũ giác ABCFG có chu vi bằng 100 + 4 13 (cm).
Cho hình vuông ABCD có bốn đỉnh nằm trên đường tròn (O;\(3\sqrt{2}\)cm) Diện tích của hình vuông ABCD là
Cho hình vuông abcd gọi e là trung điểm cạnh ab biết bán kính đường tròn ngoại tiếp Tam giác edc bằng r tính độ dài các cạnh hình vuông abcd theo r
Cho hình vuông ABCD cạnh a.Gọi O là tâm đường tròn ngoại tiếp hình vuông. Tính bán kính R của (O)?
A. R = a 2 4
B. R = a 2
C. R = O A = a 2 2
D. R = a 2
Hai hình chữ nhật abcd và amnp có phần trung là hình vuông amod tìm diện tích hình vuông amod biết hai hình chữ nhật abcd và amnp có diện tích hơn kém nhau 120 m vuông và chu vi kém nhau 20 m
Cho hình vuông ABCD nội tiếp đưòng tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đuờng tròn đó, EF là dây song song với AB. Cho hình đó quay xung quanh trục GO. Chứng minh:
a, Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra
b, Bình phương diện tích toàn phần của hình trụ bằng tích diện tích hình cầu và diện tích toàn phần của hình nón
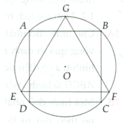
Cho hình vuông ABCD có tâm O. Gọi R,r là bán kính đường tròn ngoại tiếp và nội tiếp hình vuông ABCD.Kẻ OH⊥CD,chứng minh OH=HD