Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA2
α
Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với đáy (ABCD) và SA=2 α Tính cosin của góc giữa đường thẳng SB và mặt phẳng (SAD)
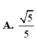
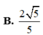
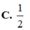
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, SAa và SA vuông góc với đáy. Tang của góc giữa đường thẳng SO và mặt phẳng (SAB) bằng A.
2
B.
2
2
C.
5
D.
5
5
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, SA=a và SA vuông góc với đáy. Tang của góc giữa đường thẳng SO và mặt phẳng (SAB) bằng
A. 2
B. 2 2
C. 5
D. 5 5
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng DE. Thể tích của khối đa diện ABCDSEF bằng A.
7
6
B.
11
12
C.
2
3
D.
5
6
Đọc tiếp
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng DE. Thể tích của khối đa diện ABCDSEF bằng
A. 7 6
B. 11 12
C. 2 3
D. 5 6
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng DE. Thể tích của khối đa diện ABCDSEF bằng A.
7
6
B.
11
12
C.
2
3
D.
5
6
Đọc tiếp
Cho hai hình vuông ABCD và ABEF có cạnh bằng 1, lần lượt nằm trên hai mặt phẳng vuông góc với nhau. Gọi S là điểm đối xứng với B qua đường thẳng DE. Thể tích của khối đa diện ABCDSEF bằng
A. 7 6
B. 11 12
C. 2 3
D. 5 6
Cho hình vuông ABCD cạnh a. Từ tâm O của hình vuông dựng đường thẳng Δ vuông góc với mặt phẳng (ABCD). Trên Δ lấy điểm S sao cho OS = a/2 . Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.
Trong mặt phẳng (
α
) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với (
α
) ta lấy một điểm S tùy ý, dựng mặt phẳng (
β
) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng (
β
) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Chứng minh rằng các điểm A, B, C, D, B’, C’ , D’ luôn luôn thuộc một mặt cầu cố định.
Đọc tiếp
Trong mặt phẳng ( α ) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với ( α ) ta lấy một điểm S tùy ý, dựng mặt phẳng ( β ) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng ( β ) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Chứng minh rằng các điểm A, B, C, D, B’, C’ , D’ luôn luôn thuộc một mặt cầu cố định.
Trong mặt phẳng (
α
) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với (
α
) ta lấy một điểm S tùy ý, dựng mặt phẳng (
β
) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng (
β
) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Tính diện tích của mặt cầu đó và tính thể tích khối cầu được tạo thành.
Đọc tiếp
Trong mặt phẳng ( α ) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với ( α ) ta lấy một điểm S tùy ý, dựng mặt phẳng ( β ) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng ( β ) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Tính diện tích của mặt cầu đó và tính thể tích khối cầu được tạo thành.
Cho hình chóp tứ giác đều
S
.
A
B
C
D
có cạnh đáy bằng a tâm O. Gọi M, N lần lượt là trung điểm của SA và BC. Góc giữa đường thẳng MN và mặt phẳng
A
B
C
D
bằng
60
0
. Tính cosin góc giữa đường thẳng và mặt phẳng
(
S
B
D
)
.
Đọc tiếp
Cho hình chóp tứ giác đều S . A B C D có cạnh đáy bằng a tâm O. Gọi M, N lần lượt là trung điểm của SA và BC. Góc giữa đường thẳng MN và mặt phẳng A B C D bằng 60 0 . Tính cosin góc giữa đường thẳng và mặt phẳng ( S B D ) .
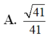
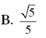
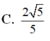
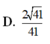
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, cạnh bên SAa
5
, mặt bên SAB là tam giác cân đỉnh S và thuộc mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SC bằng:
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, cạnh bên SA=a 5 , mặt bên SAB là tam giác cân đỉnh S và thuộc mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng AD và SC bằng: