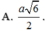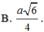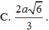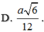

Mặt khác 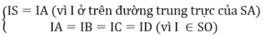
Suy ra Í=IIA=IB=IC=ID=3a/4
Vậy mặt cầu ngoại tiếp hình chóp S.ABCD có tâm I và bán kính R=SI=3a/4
Diện tích mắt cầu là:
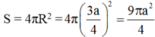
Thể tích khối cầu là:
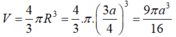


Mặt khác 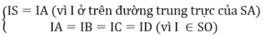
Suy ra Í=IIA=IB=IC=ID=3a/4
Vậy mặt cầu ngoại tiếp hình chóp S.ABCD có tâm I và bán kính R=SI=3a/4
Diện tích mắt cầu là:
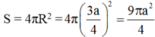
Thể tích khối cầu là:
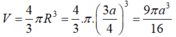
Trong mặt phẳng ( α ) cho hình vuông ABCD có cạnh bằng a. Trên đường thẳng Ax vuông góc với ( α ) ta lấy một điểm S tùy ý, dựng mặt phẳng ( β ) đi qua A và vuông góc với đường thẳng SC. Mặt phẳng ( β ) cắt SB, SC, SD lần lượt tại B’ , C’, D’. Tính diện tích của mặt cầu đó và tính thể tích khối cầu được tạo thành.
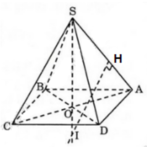
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a. Hình chiếu vuông góc của S trên mặt phẳng đáy ABCD là điểm H thuộc cạnh AB sao cho HB=2HA. Cạnh SA hợp với mặt phẳng đáy góc 60 ° . Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABCD
![]()
![]()
![]()
![]()
Cho khối chóp tứ giác đều S.ABCD có ABCD là hình vuông cạnh 2 a . Góc giữa đường thẳng SA và mặt phẳng (ABCD) bằng 60 o . Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.ABCD ?
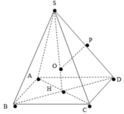
A. R = 2 a
B. R = a
C. R = 2 3 3 a
D. R = 3 2 a
Cho hình chóp tứ giác đều S.ABCD có ABCD là hình vuông cạnh 2 a . Góc giữa đường thẳng SA và mặt phẳng (SBD) bằng 30 o . Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.ABCD ?
A. R = 2 a
B. R = 6 3 a
C. R = 2 3 3 a
D. R = 3 2 a
Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a 3 , A D = a , S A vuông góc với mặt phẳng đáy và mặt phẳng (SBC) tạo với mặt đáy một góc 60 0 . Tính thể tích V của khối cầu ngoại tiếp khối chóp S. ABCD.
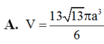

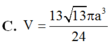
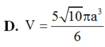
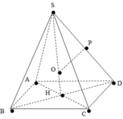
Cho hình hộp S.ABCD có ABCD là hình chữ nhật tâm I cạnh AB=3a, BC=4a. Hình chiếu của S trên mặt phẳng (ABCD) là trung điểm của ID. Biết rằng SB tạo với mặt phẳng (ABCD) một góc 45 ° . Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABCD.
![]()
![]()
![]()
![]()
Cho đường tròn tâm O bán kính r’. Xét hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy, S và A cố định, SA = h cho trước và có đáy ABCD là một tứ giác tùy ý nội tiếp đường tròn đã cho, trong đó các đường chéo AC và BD vuông góc với nhau. Tính bán kính r của mặt cầu đi qua năm đỉnh của hình chóp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 ° . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính diện tích của mặt cầu ngoại tiếp hình chóp S.ABCD.
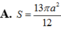
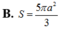
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có đường chéo bằng 2 a, cạnh SA có độ dài bằng 2a và vuông góc với mặt phẳng đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD?