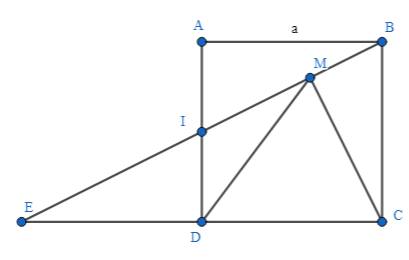
a) Vì \(E\) là điểm đối xứng với \(C\) qua \(D\Rightarrow D\) là trung điểm của \(CE\)
\(\Rightarrow MD\) là đường trung tuyến ứng với \(CE\) của \(\Delta EMC\)
Vì \(ABCD\) là hình vuông \(\Rightarrow\widehat{BCD}=90^{\circ};AB=BC=CD=DA=a\) (1)
Mà: \(\left\{{}\begin{matrix}DM=DA\left(gt\right)\\CD=DE=\dfrac{1}{2}CE\left(\text{vì D là trung điểm của CE}\right)\end{matrix}\right.\) (2)
Từ (1) và (2) \(\Rightarrow MD=\dfrac{1}{2}CE\)
Xét \(\Delta EMC\) có: \(\left\{{}\begin{matrix}\text{MD là đường trung tuyến ứng với cạnh CE}\\MD=\dfrac{1}{2}CE\end{matrix}\right.\)
\(\Rightarrow\Delta EMC\) vuông tại \(M\Rightarrow\widehat{EMC}=90^{\circ}\)
Xét \(\Delta EMC\) và \(\Delta ECB\) có: \(\left\{{}\begin{matrix}\widehat{EMC}=\widehat{ECB}=90^{\circ}\left(cmt\right)\\\widehat{E}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta EMC\sim\Delta ECB\left(g.g\right)\) (đpcm)
b) Ta có: \(\Delta EMC\sim\Delta ECB\left(cmt\right)\)\(\Rightarrow\dfrac{EC}{EB}=\dfrac{MC}{CB}\) (các cạnh tương ứng)
\(\Rightarrow EB\cdot MC=EC\cdot CB=\left(2CD\right)\cdot CB\) (vì \(CD=\dfrac{1}{2}EC\))
\(=2a\cdot a=2a^2\) ( từ (1) ) (đpcm)
c)
+, Xét \(\Delta BEC\) vuông tại \(C\) có: \(EB^2=EC^2+BC^2\) (định lí Pythagoras)
Mà: \(EC=2CD=2BC=2a;BC=a\left(cmt\right)\)
nên \(EB^2=\left(2a\right)^2+a^2=5a^2\)
+, Mặt khác: \(EB\cdot MC=2a^2\left(cmt\right)\)
\(\Rightarrow\left(EB\cdot MC\right)^2=\left(2a^2\right)^2\)
\(\Rightarrow5a^2\cdot MC^2=4a^4\)
\(\Rightarrow MC^2=\dfrac{4a^4}{5a^2}=\dfrac{4}{5}a^2\) \((*)\)
+, Vì \(\Delta EMC\sim\Delta ECB\left(cmt\right)\Rightarrow\dfrac{EM}{EC}=\dfrac{MC}{CB}\) (các cạnh tương ứng)
\(\Rightarrow\dfrac{EM}{MC}=\dfrac{EC}{CB}=\dfrac{2CD}{CB}=2\) (vì \(EC=2CD=2CB\))\(\Rightarrow EM=2MC\)
Khi đó: \(S_{\Delta EMC}=\dfrac{EM\cdot MC}{2}=\dfrac{2MC\cdot MC}{2}=MC^2\) \((**)\)
Từ \((*)\) và \((**)\Rightarrow S_{\Delta EMC}=\dfrac45 a^2\)
\(\text{#}Toru\)













