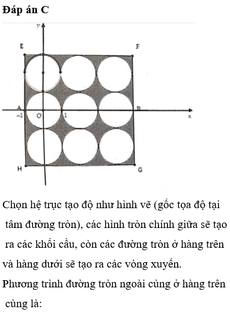
Các câu hỏi tương tự
Cho hình vẽ dưới đây trong đó A, B, C, D lần lượt là tâm của bốn đường tròn có bán kính bằng nhau, chúng tạo thành một hình vuông có cạnh là 4. Bốn đường tròn nhỏ bằng nhau và tâm của nó nằm trên các cạnh của hình vuông ABCD và mồi đường tròn này tiếp xúc với hai đường tròn lớn. Tìm diện tích lớn nhất của phần in đậm A. 5.38 B. 7.62 C. 5.98 D. 4.44
Đọc tiếp
Cho hình vẽ dưới đây trong đó A, B, C, D lần lượt là tâm của bốn đường tròn có bán kính bằng nhau, chúng tạo thành một hình vuông có cạnh là 4. Bốn đường tròn nhỏ bằng nhau và tâm của nó nằm trên các cạnh của hình vuông ABCD và mồi đường tròn này tiếp xúc với hai đường tròn lớn. Tìm diện tích lớn nhất của phần in đậm
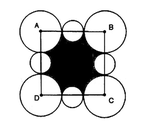
A. 5.38
B. 7.62
C. 5.98
D. 4.44
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần màu vàng nhạt (hình vẽ bên dưới) quay quanh đường thẳng AD bằng A.
23
π
a
3
3
216
B.
π
a
3...
Đọc tiếp
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần màu vàng nhạt (hình vẽ bên dưới) quay quanh đường thẳng AD bằng
A. 23 π a 3 3 216
B. π a 3 3 24
C. 20 π a 3 3 217
D. 4 π a 3 3 27
Cho hình thang ABCD vuông A và B với
A
B
B
C
A
D
2
a
. Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành. A.
V
4
πa
3
3
B.
V...
Đọc tiếp
Cho hình thang ABCD vuông A và B với A B = B C = A D 2 = a . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành.
A. V = 4 πa 3 3
B. V = 5 πa 3 3
C. V = 7 πa 3 3
D. V = πa 3
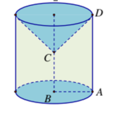
Trong mặt phẳng (P) cho hình vuông ABCD có cạnh bằng 5 và đường tròn (C) có tâm A, đường kính 10. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh trục là đường AC. A.
1000
π
+
375
π
2
6
B.
1000
π
+...
Đọc tiếp
Trong mặt phẳng (P) cho hình vuông ABCD có cạnh bằng 5 và đường tròn (C) có tâm A, đường kính 10. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh trục là đường AC.
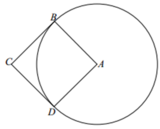
A. 1000 π + 375 π 2 6
B. 1000 π + 375 π 2 6
C. 500 π + 125 π 2 6
D. 500 π + 375 π 2 6
Cho hình thang ABCD vuông tại A và B với
A
B
B
C
A
D
2
a
.
Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành. A.
V
4
π
a
3...
Đọc tiếp
Cho hình thang ABCD vuông tại A và B với A B = B C = A D 2 = a . Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Tính thể tích V của khối tròn xoay được tạo thành.
A. V = 4 π a 3 3
B. V = 5 π a 3 3
C. V = π a 3
D. V = 7 π a 3 3
Cho hình vuông ABCD có cạnh a, M là trung điểm của AD. Xét khối tròn xoay sinh bởi tam giác CDM (cùng các điểm trong của nó) khi quay quanh đường thẳng AB. Thể tích của khối tròn xoay đó bằng A.
5
πa
3
12
B.
3
πa
3
4
C.
7...
Đọc tiếp
Cho hình vuông ABCD có cạnh a, M là trung điểm của AD. Xét khối tròn xoay sinh bởi tam giác CDM (cùng các điểm trong của nó) khi quay quanh đường thẳng AB. Thể tích của khối tròn xoay đó bằng
A. 5 πa 3 12
B. 3 πa 3 4
C. 7 πa 3 12
D. πa 3 3
Cho hàm số
y
f
x
a
x
3
+
b
x
2
+
c
x
+
d
a
,
b
,
c
,
d
∈
ℝ...
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 2 + c x + d a , b , c , d ∈ ℝ , a ≠ 0 có đồ thị (C). Biết rằng đồ thị (C) tiếp xúc với đường thẳng y = 4 tại điểm có hoành độ âm và đồ thị của hàm số y = f ' x cho bởi hình vẽ dưới đây. Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng H giời hạn bởi đồ thị (C) và trục hoành xung quanh trục hoành Ox
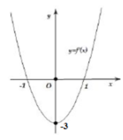
A. 725 35 π
B. 1 35 π
C. 6 π
D. Đáp án khác
Cho mô hình (như hình vẽ) với tam giác EFB vuông tại B, cạnh FB a,
E
F
B
^
30
°
và tứ giác ABCD là hình vuông. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh cạnh AF A.
V
4
/
3
a
3
B. V 10/9
a
3
C....
Đọc tiếp
Cho mô hình (như hình vẽ) với tam giác EFB vuông tại B, cạnh FB= a, E F B ^ = 30 ° và tứ giác ABCD là hình vuông. Tính thể tích V của vật thể tròn xoay được tạo thành khi quay mô hình quanh cạnh AF
A. V = 4 / 3 a 3
B. V= 10/9 a 3
C. V= 4/3 π a 3
D. V= 10/9 π a 3
Trong không gian cho tam giác OIM vuông tại I,
I
O
M
45
°
và cạnh IM a Khi quay tam giác IOM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Khi đó diện tích xung quanh của hình nón tròn xoay đó bằng: A.
π
a
2
3
B.
π
a
2
C....
Đọc tiếp
Trong không gian cho tam giác OIM vuông tại I, I O M = 45 ° và cạnh IM = a Khi quay tam giác IOM quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình nón tròn xoay. Khi đó diện tích xung quanh của hình nón tròn xoay đó bằng:
A. π a 2 3
B. π a 2
C. π a 2 2
D. π a 2 2 2