\(DA=\sqrt{AE^2+DE^2}\approx3,9\left(m\right)\)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hình vẽ. Độ dài cạnh DA là: a)6,4 B)3,6 C)7,2 D)5,4
vẽ hình hộ mình đề này Cho hình vuông ABCD có độ dài cạnh bằng 4cm. Vẽ đường tròn tâm O đường kính AD, kẻ BM là tiếp tuyến của đường tròn O ( M là tiếp điểm, M khác A), BM cắt CD tại K a) Cm 4 điểm A,B,M,O cùng thuộc 1 đg tròn ( cm: 2 tam nội tiếp) b) Chứng minh OB vuông góc OK và BM.MK A...
Đọc tiếp
vẽ hình hộ mình đề này Cho hình vuông ABCD có độ dài cạnh bằng 4cm. Vẽ đường tròn tâm O đường kính AD, kẻ BM là tiếp tuyến của đường tròn O ( M là tiếp điểm, M khác A), BM cắt CD tại K a) Cm 4 điểm A,B,M,O cùng thuộc 1 đg tròn ( cm: 2 tam nội tiếp) b) Chứng minh OB vuông góc OK và BM.MK= AB^2/4 c) Đường thẳng AM cắt CD tại E. Cm K là trung điểm của ED và tính chu vi tứ giác ABKD
Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là B, C, D, A theo đúng kích thước đã cho (cạnh hình vuông ABCD dài 1cm). Nêu cách vẽ đường xoắn AEFGH. Tính độ dài đường xoắn đó.
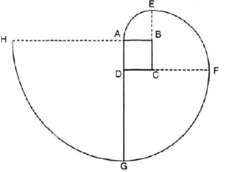
Hình 55
Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là B, C, D, A theo đúng kích thước đã cho (cạnh hình vuông ABCD dài 1cm). Nêu cách vẽ đường xoắn AEFGH. Tính độ dài đường xoắn đó.
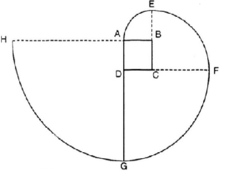
Cho hcn ABCD . Lấy E,F thuộc cạnh AB ; G,H thuộc BC ; I,J thuộc CD; K,M thuộc DA sao cho hình 8-giác EFGHIJKM có các góc bằng nhau. CMR: Nếu độ dài cạnh 8-giác ABCD là số hữu tỉ thì EF = IJ
cho hình vuông có độ dài là đường chéo là 1.Trên mỗi cạnh của hình vuông các điểm M,N,P,Q. (M THUỘC AB,N THUỘC BC,P THUỘC cp,q thuộc da)CMR: chu vi tứ giác MNPQ lớn hơn hoặc bằn 2
Cho hình vuông ABCD có độ dài cạnh là 10cm. Gọi E, F, G, H là các trung điểm của AB, BC, CD và DA. Tính diện tích phần được tô màu.
Cho Tam giác ABC vuông tại A, biết AB = 12, BC = 15.
a) vẽ hình và tính độ dài AC
b) tính tanB và số đo góc C trong tam giác ABC ( làm tròn đến độ)
c) vẽ tia phân giác CD của góc C , điểm Đ thuộc AB. Chúng minh: BC là tiếp tuyến của đường tròn ( D; DA)
Cho hình vuông ABCD có độ dài cạnh là 1. M là trung điểm của CD. AM cắt BD tại P, BM cắt AC tại Q. O là giao của AC và BD. Hãy tính diện tích hình MPOQ (xem hình vẽ).
ABCDMOPQ










