Các câu hỏi tương tự
cho hình thang ABCD ,M là điểm tùy ý trên đáy lớn AB , Từ M kẻ ME // AC và MF // BD (E thuộc BC ,F thuộc AD ). EF cắt AC và BD lần lượt tại I và J .
a, CMR : Nếu H là trung điểm của IJ thì H cũng là trung điểm của FE
b, Giả sử AB=2CD, xác định vị trí của M sao cho JE=IJ=IF.
cho hình thang ABCD,M là một điểm tùy ý trên đáy lớn AB. từ M kẻ các đường thẳng // vs 2 đường chéo AC và BD, các đường thẳng này cắt 2 cạnh BC,AD lần lượt tại E,F. Đoạn EF cắt AC và BD tại I và J
a) CM Nếu H là trug điểm của IJ thì H cũng là trung điểm của EF
b) Trong trương hợp AB=2CD, hảy chỉ ra vị trí của M trên AB sao cho
EJ=IJ=IF
cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau;a)Gọi E,F,G,H tương ứng là trung điểm các cạnh AB,BC,CD,DA.Chứng minh rằng EFGH là hình chữ nhậtb) Gọi I,J,K,L tương ứng là trung điểm các cạnh EF,FG,GH,HE nói ở câu a). Chứng minh rằng IJHL là hình thoic)Gọi M,N,P,Q tương ứng là trung điểm các cạnh IJ,JK,KL,LI nói ở câu b).Chứng minh rằng MNPQ là hình vuôngd) Khi AC vuông góc với BD và ACBD thì các tứ giác EFGH, IJKL,MNPQ là hình gì? Vì sao?
Đọc tiếp
cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau;
a)Gọi E,F,G,H tương ứng là trung điểm các cạnh AB,BC,CD,DA.Chứng minh rằng EFGH là hình chữ nhật
b) Gọi I,J,K,L tương ứng là trung điểm các cạnh EF,FG,GH,HE nói ở câu a). Chứng minh rằng IJHL là hình thoi
c)Gọi M,N,P,Q tương ứng là trung điểm các cạnh IJ,JK,KL,LI nói ở câu b).Chứng minh rằng MNPQ là hình vuông
d) Khi AC vuông góc với BD và AC=BD thì các tứ giác EFGH, IJKL,MNPQ là hình gì? Vì sao?
Bài 2: Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau.a) Gọi E,F,G,H tương ứng là trung điểm các cạnhAB, BC,CD,DA. Chứng minh rằng EFGH là hình chữ nhât,b) Gọi I,J,K,L là trung điểm các cạnh EF,FG,GH,HE nói ở câu a. Chứng minh IJKL là hình thoi.c) Gọi M,N,P,Q tương ứng là trung điểm các cạnh IJ,JK,KL,LI Nói ở câu n, Chứng minh rằng MNPQ là hình thoid) Khi AC vuông góc với BD và AC BD thì các tứ giác EFGH, IJKL,MNPQ là hình gì ?vì sao?AI TRẢ LỜI GIÚP MK, MK TICK CHO HẾT ! GIÚP MIN...
Đọc tiếp
Bài 2: Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau.
a) Gọi E,F,G,H tương ứng là trung điểm các cạnhAB, BC,CD,DA. Chứng minh rằng EFGH là hình chữ nhât,
b) Gọi I,J,K,L là trung điểm các cạnh EF,FG,GH,HE nói ở câu a. Chứng minh IJKL là hình thoi.
c) Gọi M,N,P,Q tương ứng là trung điểm các cạnh IJ,JK,KL,LI Nói ở câu n, Chứng minh rằng MNPQ là hình thoi
d) Khi AC vuông góc với BD và AC =BD thì các tứ giác EFGH, IJKL,MNPQ là hình gì ?vì sao?
AI TRẢ LỜI GIÚP MK, MK TICK CHO HẾT ! GIÚP MINH NHA!:(
Hôm nay là ngày lễ, chắc các bạn có thời gian rảnh, mk giới thiệu một số bài toán khó sau (lớp 8):1/ Tìm GTLN của biểu thức: Afrac{27-12x}{x^2+9}2/ Cho hình thang ABCD, M là một điểm bất kì trên đáy lớn AB. Từ M vẽ ME song song với AC, E thuộc BC; MF song song với BD, F thuộc AD. EF cắt AC và BD tại I và J.a) CMR: Nếu H là trung điểm IJ thì H cũng là trung điểm của EF.b) Nếu AB 2.CD, xác định vị trí điểm M trên AB sao cho EJJIIF.3/ Cho tam giác ABC vuông tại A và điểm H di chuyển trên BC. Gọi...
Đọc tiếp
Hôm nay là ngày lễ, chắc các bạn có thời gian rảnh, mk giới thiệu một số bài toán khó sau (lớp 8):
1/ Tìm GTLN của biểu thức: \(A=\frac{27-12x}{x^2+9}\)
2/ Cho hình thang ABCD, M là một điểm bất kì trên đáy lớn AB. Từ M vẽ ME song song với AC, E thuộc BC; MF song song với BD, F thuộc AD. EF cắt AC và BD tại I và J.
a) CMR: Nếu H là trung điểm IJ thì H cũng là trung điểm của EF.
b) Nếu AB = 2.CD, xác định vị trí điểm M trên AB sao cho EJ=JI=IF.
3/ Cho tam giác ABC vuông tại A và điểm H di chuyển trên BC. Gọi E,F lần lượt là điểm đối xứng với H qua AB và AC.
a) CMR: E, A, F thẳng hàng.
b) CMR: BEFC là hình thang.
c) Xác định vị trí của H để tam giác EHF có diện tích lớn nhất.
BẠN NÀO LÀM ĐƯỢC 1 TRONG 3 BÀI SẼ ĐƯỢC TICK.
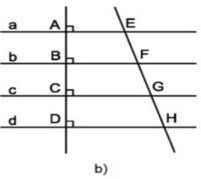
Cho hình 96b, trong đó các đường thẳng a, b, c, d song song với nhau.
Chứng minh rằng:
a) Nếu các đường thẳng a, b, c, d song song cách đều thì EF = FG = GH.
b) Nếu EF = FG = GH thì các đường thẳng a, b, c, d song song cách đều.
Cho hình vuông EFGH 1 góc vuông xEy thay đổi quay quanh E Ex cắt FG, GH tại M,n Ey cắt FG, GH tại P,Q
a) Chứng minh tam giác ENP,EMQ là tam giác cân
b QM cắt NP tại R. I,K là trung điểm của PN và QM tứ giác EKRY là hình gì
c) Chứng minh F,H,K,I thẳng hàng
Cho hình chũ nhật ABCD, E thuộc đường chéo BD. Trên tia đối của tia EC lấy điểm F sao cho CE = EF. Vẽ FG vuông góc AB tại G, FH vuông góc AD tại H
a) Chứng minh rằng tứ giác AHFG là hình chũ nhật
b) AF // BD
c) E, G, H thẳng hàng
cho hình vuông EFGH , một góc vuông xEy quay quanh E có Ex cắt FG và GH tại M , N và Ey cắt FG và GH tại P , Q
a) Chứng minh tam giác EMQ và tam giác ENP vuông cân
b) Gọi R là giao điểm của QM và NP ; I , K lần lượt là trung điểm của PN , QM . Tứ giác EKRI là hình gì , vì sao
c) Chứng minh F , H , K , I thẳng hàng