a, Do N là trung điểm của CD ⇒ N ∈ (ACD).
Ta có N ∈ (ABN).
Mặt khác: A ∈ (ACD) và A ∈ (ABN)
⇒ (ACD) \(\cap\) (ABN) = AN
b, Do N ∈ CD ⇒ N ∈ (CDM). Hiển nhiên : N ∈ (ABN)
Do M ∈ AB nên M ∈ (ABN). Hiển nhiên : M ∈ (CDM)
⇒ (ABN) \(\cap\) (CDM) = MN

a, Do N là trung điểm của CD ⇒ N ∈ (ACD).
Ta có N ∈ (ABN).
Mặt khác: A ∈ (ACD) và A ∈ (ABN)
⇒ (ACD) \(\cap\) (ABN) = AN
b, Do N ∈ CD ⇒ N ∈ (CDM). Hiển nhiên : N ∈ (ABN)
Do M ∈ AB nên M ∈ (ABN). Hiển nhiên : M ∈ (CDM)
⇒ (ABN) \(\cap\) (CDM) = MN
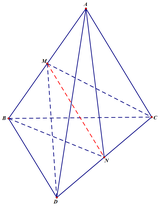
Cho tứ diện ABCD có ba cặp cạnh đối diện bằng nhau là AB = CD, AC = BD và AD = BC. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh MN ⊥ AB và MN ⊥ CD. Mặt phẳng (CDM) có vuông góc với mặt phẳng (ABN) không? Vì sao?
Bt2: cho hình chóp S.ABCD đáy là tứ giác lồi có AB>CD .gọi M,N lần lượt là trung điểm của cạnh SA và SD .a) tìm giao tuyến (SAB) và (SCD).b) tìm giao tuyến của (MNC) và (ABCD).c)tìm giao điểm của MN và (ABN).d) tìm thiết diện của hình chóp vs mp (BMN)
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AC và BC, P là điểm thuộc DB sao cho PB = 2PD. Gọi Q là giao điểm của CD với mặt phẳng (MNP). Giao tuyến của hai mặt phẳng (MNP) và (ACD) là:
A. MP
B. NQ
C. MQ
D. AP
Cho tứ diện ABCD. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, BD,CD.
a. Xác định giao tuyến của hai mặt phẳng (AMN) và (ACD).
b. Chứng minh rằng đường thẳng BC song song với mặt phẳng (ANP)
c. Gọi G, H lần lượt là trọng tâm của tam giác ABC và ACD. Chứng minh GH // BD.
Cho tứ diện ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD, trên cạnh AD lấy điểm P không trùng với trung điểm của AD.
a) Gọi E là giao điểm của đường thẳng MP và đường thẳng BD. Tìm giao tuyến của hai mặt phẳng (PMN) và (BCD).
b) Tìm giao điểm của hai mặt phẳng (PMN) và BC.
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Trên cạnh CD lấy
điểm P sao cho PD=2PC .
a) Tìm giao điểm của đường thẳng BD và mặt phẳng (MNP).
b) Tìm giao tuyến của mặt phẳng (MNP) và (ABD).
Cho tứ diện ABCD và điểm M thuộc miền trong của tam giác ACD. Gọi I và J lần lượt là 2 điểm trên cạnh BC và BD sao cho IJ không song song với CD. Gọi H và K lần lượt là giao điểm của IJ và CD; MH và AC. giao tuyến của 2 mặt phẳng (ACD) và (IJM) là
A. KI
B. KJ
C. MI
D. MH
Cho tứ diện ABCD. Trên cạnh AB lấy điểm I và lấy các điểm J, K lần lượt là điểm thuộc miền trong các tam giác BCD và ACD. Gọi L là giao điểm của JK với mặt phẳng (ABC)
a) Hãy xác định điểm L.
b) Tìm giao tuyến của mặt phẳng (IJK) với các mặt của tứ diện ABCD.
Cho tứ diện ABCD. Gọi IJ lần lượt là trung điểm của BC và BD. Giao tuyến của hai mặt phẳng (AIJ) và (ACD) là đường nào sau đây?
A. đường thẳng d đi qua A và d // BC.
B. đường thẳng d đi qua A và d // BD.
C. đường thẳng d đi qua A và d // CD.
D. đường thẳng d đi qua A, M trong đó M là giao điểm IJ và CD.