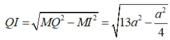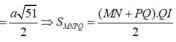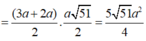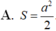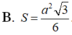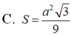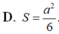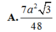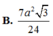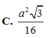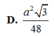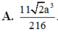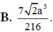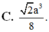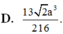Đáp án là D
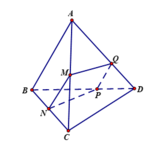
Trong mặt phẳng (ABD) qua P kẻ đường thẳng song song AB cắt AD tại Q ta có
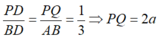
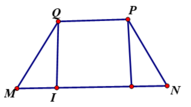
Dễ thấy MN là đường trung bình tam giác ABC nên MN//AB//PQ,nên 4 điểm M,N,P,Q đồng phẳng và MN=3a, thiết diện cần tim chính là hinh thang MNPQ, do tất cả các cạnh cạnh của tứ diện bằng 6a nên tam giác BNP = tam giác AMQ => NP = MQ vậy MNPQ là hình thang cân, ta có
![]()
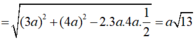
Kẻ đường cao QI có