Đáp án C
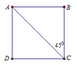
Vì ABCD là hình chữ nhật và A C B ⏜ = 45 ° nên ABCD là hình vuông.
Ta có: 2. A B 2 = 2 3 a 2 ⇔ A B = 6 a
S t p = 2 π B C 2 + 2 π . B C = 2 π . B C . A B = 2 π . 6 a 2 + 2 π . 6 a 2 = 24 π a 2
Đáp án C

Vì ABCD là hình chữ nhật và A C B ⏜ = 45 ° nên ABCD là hình vuông.
Ta có: 2. A B 2 = 2 3 a 2 ⇔ A B = 6 a
S t p = 2 π B C 2 + 2 π . B C = 2 π . B C . A B = 2 π . 6 a 2 + 2 π . 6 a 2 = 24 π a 2
Hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD xung quanh cạnh AB. Biết A C = 2 a 2 và A C B ^ = 45 ° . Diện tích toàn phần của hình trụ (T) bằng
A. 10 πa 2
B. 16 πa 2
C. 12 πa 2
D. 8 πa 2
Hình trụ (T) được sinh ra khi quay hình chữ nhật ABCD quanh cạnh AB. Biết A C = 2 a 2 và A C B ^ = 45 0 . Diện tích toàn phần S t p của hình trụ (T) là
A. S t p = 16 π a 2 .
B. S t p = 10 π a 2 .
C. S t p = 12 π a 2 .
D. S t p = 8 π a 2 .
Cho hình chữ nhật ABCD có AB=a, AC=2a. Tính diện tích xung quanh của hình trụ nhận được khi quay hình chữ nhật quanh cạnh AB
A. a 2 2 3 3
B. 3 a 2
C. 2 3 a 2
D. 2 3 π a 2
Cho hình vuông ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của AB và CD. Khi quay hình vuông ABCD quanh MN thành một hình trụ. Gọi (S) là mặt cầu có diện tích bằng diện tích toàn phần của hình trụ, ta có bán kính của mặt cầu (S) là:
A. a 6 3
B. a 6 2
C. a 6 4
D. a 6
Cho hai điểm A, B thuộc đồ thị hàm số y = sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD = 2 π /3. Độ dài của cạnh BC bằng
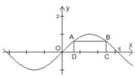
A. 2 2
B. 1 2
C. 1
D. 3 2
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AD=8,CD=6,AC'=12. Tính diện tích toàn phần S t p của hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hình chữ nhật ABCD và A′B′C′D′.
A. S t p = 576 π
B. S t p = 10 2 11 + 5 π
C. S t p = 26 π
D. S t p = 5 4 11 + 5 π
Cho hình chữ nhật ABCD có chiều dài A B = 2 A D . Quay hình chữ nhật quay quanh cạnh AB sinh ra khối trụ có thể tích V 1 và quay hình chữ nhật đó quanh cạnh AD sinh ra hình
trụ có thể tích V 2 . Tỉ số V 1 V 2 là
A. 27 π 2 .
B. 1 2 .
C. π 2 .
D. 27
Trong không gian cho hình chữ nhật ABCD có AB = 1. AD = 2. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN ta được một hình trụ. Tính diện tích toàn phần của hình trụ đó?
A. 10 π
B. 4 π
C. 2 π
D. 6 π
Trong không gian, cho hình chữ nhật ABCD có A B = 1 và A D = 2. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần S t p của hình trụ đó.
A. S t p = 4 3 π
B. S t p = 4 π
C. S t p = 6 π
D. S t p = 3 π