Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Cho đa giác đều có 10 đỉnh.Tìm số véc tơ khác véc tơ 0 có điểm đầu và điểm cuối là đỉnh của các đa giác
Cho hình thoi ABCD có đỉnh A(0;1). Đường chéo BD có phương trình \(x+2y-7=0\) . Cạnh AB có phương trình là \(x+7y-7=0\). Tìm tọa độ các đỉnh B, C, D của hình thoi.
Trong mặt phẳng tọa độ Oxy. Cho hình thoi ABCD cạnh a và
B
A
D
^
60
°
. Biết A trùng với gốc tọa độ O; C thuộc trục Ox và xB; yB ≥ 0. Tìm tọa độ các đỉnh B và C của hình thoi ABCD. A. B. C. D.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy. Cho hình thoi ABCD cạnh a và B A D ^ = 60 ° . Biết A trùng với gốc tọa độ O; C thuộc trục Ox và xB; yB ≥ 0. Tìm tọa độ các đỉnh B và C của hình thoi ABCD.
A. 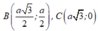
B. 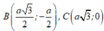
C. 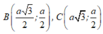
D. 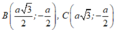
Trong mặt phẳng cho 10 điểm A,Az;A:AriAs;AA);AA);A, đôi một không trung nhau. Hỏi thành lập được bao véc tơ có các điểm đầu và điểm cuối là các điểm đó.
Cho hình thoi ABCD tâm I. Biết hai cạnh AB và AD lần lượt có phương trình là 2x - y - 1 = 0 và x - 2y - 5 = 0 , tâm I thuộc Parabol y ^ 2 = x . Tính toạ độ các đỉnh của hình thoi.
Cho một hình chữ nhật ABCD. Số vectơ khác 0 → mà điểm đầu và điểm cuối trùng với các đỉnh của hình chữ nhật là:
A. 4
B. 6
C. 12
D. 16
cho hình bình hành ABCD. m là rung điểm AD,N là trung điểm BC. tính vé tơ AD+ véc tơ Mb + véc tơ NA
Cho hình bình hành ABCD tâm O. Gọi I là trung điểm của CD và G là trọng tâm của tam giác ABD. Phân tích véc tơ IG theo 2 véc tơ AB ; AD
Cho hình thoi ABCD có góc tại đỉnh A nhọn. Khẳng định nào sau đây là đúng? A.
A
B
→
B
C
→
B.
A
B
→
B
C
→
C. ...
Đọc tiếp
Cho hình thoi ABCD có góc tại đỉnh A nhọn. Khẳng định nào sau đây là đúng?
A. A B → = B C →
B. A B → = B C →
C. A B → = C D →
D. A B → = - C D →








