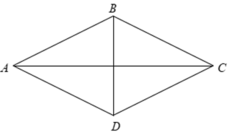
Xét hình thoi ABCD có BACˆ = 600.
Ta có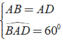 ⇒ Δ ABD đều.
⇒ Δ ABD đều.
⇒ AB = AD = BD = 4cm
Gọi H là giao điểm của hai đường chéo AC,BD.
Áp dụng định lí Py – to – go ta có:
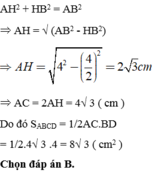

Xét hình thoi ABCD có BACˆ = 600.
Ta có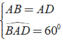 ⇒ Δ ABD đều.
⇒ Δ ABD đều.
⇒ AB = AD = BD = 4cm
Gọi H là giao điểm của hai đường chéo AC,BD.
Áp dụng định lí Py – to – go ta có:
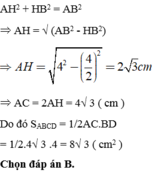
Cho hình thang ABCD ( A B / / C D ) c ó A B = A D = C D / 2 . Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.
Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD. a) Chứng minh tứ giác ABMD là hình thoi b) Chứng minh BD ⊥ BC c) Chứng minh ΔAHD và ΔCBD đồng dạng d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.
Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD
Cho hình thang cân ABCD có AB song song CD,ad = ab = A ,góc ADC = 60° A,B.C,D là trung điểm của AB, BC ,CD, DA
a/ Tính diện tích hình thang ABCD
b/Chứng minh A,B,C,D là hình thoi
Cho hình thang ABCD c ó A B = A D = 1/2 DC . Gọi M là trung điểm của CD và H là giao điểm của AM và BD. a) Chứng minh tứ giác ABMD là hình thoi b) Chứng minh BD ⊥ BC c) Chứng minh ΔAHD và ΔCBD đồng dạng d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.
cho hình thoi ABCD có AC= 9cm BD= 6cm ta gọi M,N,P,Q lần lượt là trung điểm của các đoạn thẳng AB BC CD DA
a) CMR: MNPQ là hình chữ nhật
b) tính tỉ số diện tích của hình chữ nhật MNPQ với diện tích hình thoi ABCD
c) tính diện tích tam giác BMN
1.Cho hình thoi ABCD có cạnh =a.Biết góc B=60 độ
a)C/m tam giác ABC đều
b)Tính diện tích hình thoi ABCD theo a
2.Cho hình vuông ABCD có độ dài cạnh =a.Điểm M bất kì trên đường thẳng AC.Kẻ ME vuông góc AB tại E và MF vuông góc AC tại F.Tìm vị trí của điểm M trên AC để diện tích tam giác CEF lớn nhất
cho hình thoi ABCD, AC = 9, BD = 6. M,N,P,Q lần lượt là trung điểm của AB, BC, CD, DA.
a, Cm MNPQ là hcn
b, Tính tỉ số d tích hcn MNPQ vs d tích hình thoi ABCD
c, Tính d tích tam giác BMN
cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau taị O. đường thẳng d1 qua O cắt cạnh AB và CD lần lượt tại M và P,đường thẳng d2 qua O cắt cạnh BC và DA lần lượt tại N và Q. BIẾT rằng d1 vuông góc d2.
c/m:
a, tứ giác MNPQ là hình bình hành
b, tứ giác MNPQ là hình thoi.
bài 2:cho tam giác ABC cân tại A. kẻ Bx//AC, Cy// AB, sao cho 2 tia Bx và Cy cắt nhau tại D.
1, C/M tứ giác ABCD là hình thoi
2, các đường trung tuyến BM vàCN của tam giác ABC cắt nhau ở G. AG cắt BC tại O. c/m AO là đường cao của tam giác ABC.
3, C/M A,O,D thẳng hàng.
Cho hình thoi ABCD có AB = BC = CD = DA = 4cm và B A C ^ = 60 0 . Diện tích của hình thoi ABCD là
A. 8 c m 2
B. 8 3 c m 2
C. 16 c m 2
D. 15 c m 2