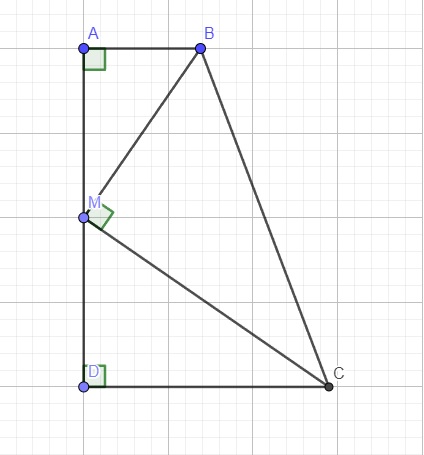
a.
M là trung điểm AD \(\Rightarrow AM=DM=\dfrac{AD}{2}=a\)
Do \(\widehat{A}=90^0\Rightarrow\widehat{ABM}+\widehat{AMB}=90^0\)
Mà \(\widehat{AMB}+\widehat{DMC}=180^0-\widehat{BMC}=90^0\)
\(\Rightarrow\widehat{ABM}=\widehat{DMC}\)
Xét hai tam giác vuông ABM và DMC có:
\(\left\{{}\begin{matrix}\widehat{ABM}=\widehat{DMC}\left(cmt\right)\\\widehat{BAM}=\widehat{MDC}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta ABM\sim\Delta DMC\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{DM}=\dfrac{AM}{CD}\Rightarrow AB.CD=AM.DM=a^2\)
b.
Cũng từ \(\Delta ABM\sim\Delta DMC\Rightarrow\dfrac{AB}{DM}=\dfrac{BM}{CM}\)
Mà \(DM=AM\Rightarrow\dfrac{AB}{AM}=\dfrac{BM}{CM}\Rightarrow\dfrac{AB}{BM}=\dfrac{AM}{CM}\)
Xét hai tam giác ABM và MBC có:
\(\left\{{}\begin{matrix}\dfrac{AB}{BM}=\dfrac{AM}{CM}\\\widehat{BAM}=\widehat{BMC}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta ABM\sim\Delta MBC\left(c.g.c\right)\Rightarrow\widehat{ABM}=\widehat{MBC}\)
\(\Rightarrow BM\) là phân giác góc B