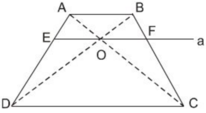
a: Xét ΔOMN và ΔOPQ có
\(\widehat{OMN}=\widehat{OPQ}\)
\(\widehat{MON}=\widehat{POQ}\)
Do đó; ΔOMN\(\sim\)ΔOPQ
Suy ra: OM/OP=ON/OQ
hay \(OM\cdot OQ=ON\cdot OP\)
b: Xét ΔMQP có AO//QP
nên AO/PQ=MA/MQ(1)
Xét ΔNQP có OB//QP
nên OB/PQ=NB/NP(2)
Xét hình thang MNPQ có AB//QP
nên MA/MQ=NB/NP(3)
Từ (1), (2) và (3) suy ra OA=OB