Các câu hỏi tương tự
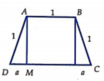
Cho hình thang cân ABCD có đáy nhỏ AB và hai cạnh bên đều có độ dài bằng 1. Tìm diện tích lớn nhất
S
m
a
x
của hình thang.
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ AB và hai cạnh bên đều có độ dài bằng 1. Tìm diện tích lớn nhất S m a x của hình thang.
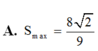
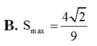
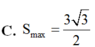
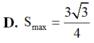
Cho hình thang cân ABCD có đáy nhỏ AB1, đáy lớn CD3, cạnh bên
A
D
2
quay quanh đường thẳng AB. Tính thể tích V của khối tròn xoay tạo thành.
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ AB=1, đáy lớn CD=3, cạnh bên A D = 2 quay quanh đường thẳng AB. Tính thể tích V của khối tròn xoay tạo thành.
![]()
![]()
![]()
![]()
Trong tất cả các hình thang cân có cạnh bên bằng 2 và cạnh đáy nhỏ bằng 4, tính chu vi P của hình thang có diện tích lớn nhất.
Đọc tiếp
Trong tất cả các hình thang cân có cạnh bên bằng 2 và cạnh đáy nhỏ bằng 4, tính chu vi P của hình thang có diện tích lớn nhất.
![]()
![]()
![]()
![]()
Trong không gian vói hệ trục tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB, CD thỏa mãn CD2AB và diện tích bằng 28, đỉnh
A
(
-
1
;
-
1
;
0
)
, phương trình đường thẳng chứa cạnh CD là
x
-
2
2
y
+
1
2...
Đọc tiếp
Trong không gian vói hệ trục tọa độ Oxyz, cho hình thang cân ABCD có hai đáy AB, CD thỏa mãn CD=2AB và diện tích bằng 28, đỉnh A ( - 1 ; - 1 ; 0 ) , phương trình đường thẳng chứa cạnh CD là x - 2 2 = y + 1 2 = z - 3 1 . Tìm tọa độ điểm D biết hoành độ điểm B lớn hơn hoành độ điểm A.
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hình thang ABCD có hai đáy AB, CD; có tọa độ ba đỉnh
A
(
1
;
2
;
1
)
,
B
(
2
;
0
;
-
1
)
,
C
(
6
;
1
;
0
)
. Biết hình thang có diện tích bằng
6
2
. Giả sử đỉnh
D
(...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hình thang ABCD có hai đáy AB, CD; có tọa độ ba đỉnh A ( 1 ; 2 ; 1 ) , B ( 2 ; 0 ; - 1 ) , C ( 6 ; 1 ; 0 ) . Biết hình thang có diện tích bằng 6 2 . Giả sử đỉnh D ( a ; b ; c ) , tìm mệnh đề đúng?
![]()
![]()
![]()
![]()
Cho hình thang vuông ABCD có đường cao AD1 , đáy nhỏ AB1, đáy lớn CD2 . Cho hình thang đó quay quanh AB ta được khối tròn xoay có thể tích bằng
Đọc tiếp
Cho hình thang vuông ABCD có đường cao AD=1 , đáy nhỏ AB=1, đáy lớn CD=2 . Cho hình thang đó quay quanh AB ta được khối tròn xoay có thể tích bằng
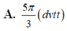
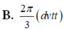
![]()
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB a, cạnh đáy CD 2a, AD a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng
3
a
2
2
. Thể tích của hình chóp S.ABCD bằng:A.
a
3
B.
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
Cho hình thang cân ABCD; AB//CD; AB2; CD4. Khi quay hình thang quanh trục CD thu được một khối tròn xoay có thể tích bằng
6
π
. Diện tích hình thang ABCD bằng: A.
9
2
B.
9
4
C. 6 D. 3
Đọc tiếp
Cho hình thang cân ABCD; AB//CD; AB=2; CD=4. Khi quay hình thang quanh trục CD thu được một khối tròn xoay có thể tích bằng 6 π . Diện tích hình thang ABCD bằng:
A. 9 2
B. 9 4
C. 6
D. 3
Cho nửa đường tròn đường kính AB 2 và hai điểm C, D thay đổi trên nửa đường tròn đó sao cho ABCD là hình thang. Diện tích lớn nhất của hình thang ABCD bằng A.
1
2
B.
3
3
4
C.
1
D.
3
3
2
Đọc tiếp
Cho nửa đường tròn đường kính AB = 2 và hai điểm C, D thay đổi trên nửa đường tròn đó sao cho ABCD là hình thang. Diện tích lớn nhất của hình thang ABCD bằng
A. 1 2
B. 3 3 4
C. 1
D. 3 3 2