Cho hình thang ABCD.Hai đường chéo AC và BD cắt nhau tại điểm I.Độ dài AB = 9cm,độ dài DC = 22cm.Trên cạch DC lấy 1 điểm E sao cho CE bằng 4cm (hình vẽ bên dưới), biết diện tích tam giác BEC là 14cm2 .
a)So sánh diện tích hai tam giác AID và BIC.
b)Tính diện tích hình thang ABED.
c)Tìm tỉ số diện tích giữa tam giác ABD và tam giác BED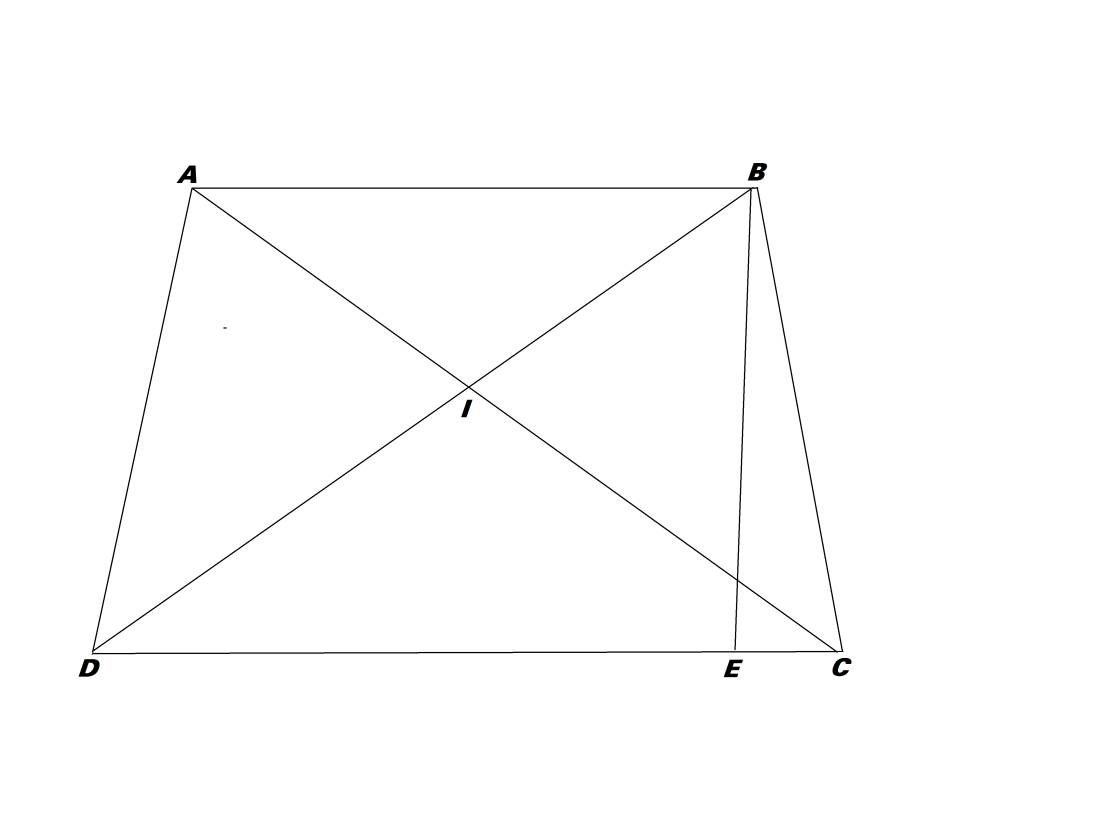
a)
\(S_{ADC}=S_{BDC}\) (vì có chung chiều cao và cạnh DC)
\(\Rightarrow S_{ADC}-S_{DIC}=S_{BDC}-S_{DIC}\)
\(\Rightarrow S_{ADI}=S_{BIC}\)
b)
Chiều cao hình thanh là:
\(\dfrac{14\times2}{4}=7\left(cm\right)\)
Diện tích hình thang ABCD là:
\(\dfrac{\left(9+22\right)\times7}{2}=108,5\left(cm^2\right)\)
c)
Độ dài DE là: \(22-4=18\left(cm\right)\)
\(\Rightarrow\dfrac{AB}{DE}=\dfrac{9}{18}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{S_{ABD}}{S_{BDE}}=\dfrac{1}{2}\) (có cùng chiều cao)











