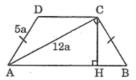
a: Ta có: \(\widehat{ADC}+\widehat{DAC}=90^0\)(ΔACD vuông tại C)
\(\widehat{ACE}+\widehat{CAD}=90^0\)(ΔCAE vuông tại E)
Do đó: \(\widehat{ADC}=\widehat{ACE}\)
b: Xét tứ giác AECB có
\(\widehat{AEC}=\widehat{ABC}=\widehat{BAE}=90^0\)
=>AECB là hình chữ nhật
=>AE=CB=4cm
Ta có: AE+EC=AD
=>ED+4=16
=>ED=12(cm)
Xét ΔCAD vuông tại C có CE là đường cao
nên \(CE^2=EA\cdot ED\)
=>\(CE=\sqrt{4\cdot12}=4\sqrt{3}\left(cm\right)\)
Xét ΔCEA vuông tại E có \(EA^2+EC^2=CA^2\)
=>\(CA=\sqrt{4^2+\left(4\sqrt{3}\right)}=8\left(cm\right)\)
Xét ΔCEA vuông tại E có
\(sinACE=\dfrac{AE}{AC}=\dfrac{4}{8}=\dfrac{1}{2}\)
=>\(sinADC=sinACE=\dfrac{1}{2}\)
\(AE\cdot AD=4\cdot16=64;AC^2=8^2=64\)
Do đó: \(AC^2=AE\cdot AD\)