Các câu hỏi tương tự
Cho khối nón có góc ở đỉnh của thiết diện qua trục là
π
3
. Một khối cầu (S1) nội tiếp trong khối nón. Gọi S2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S1; S3 là khối tiếp xúc với tất cả các đường sinh của nón và với S2; ….; Sn là khối cầu tiếp xúc với tất cả các đường sinh của nón và với Sn-1. Gọi V1, V2, V3, … , Vn-1, Vn lần lượt là thể tích của khối cầu S1, S2, S3, …, Sn-1, Sn và V là thể tích của khối nón. Tính giá trị biểu thức...
Đọc tiếp
Cho khối nón có góc ở đỉnh của thiết diện qua trục là π 3 . Một khối cầu (S1) nội tiếp trong khối nón. Gọi S2 là khối cầu tiếp xúc với tất cả các đường sinh của nón và với S1; S3 là khối tiếp xúc với tất cả các đường sinh của nón và với S2; ….; Sn là khối cầu tiếp xúc với tất cả các đường sinh của nón và với Sn-1. Gọi V1, V2, V3, … , Vn-1, Vn lần lượt là thể tích của khối cầu S1, S2, S3, …, Sn-1, Sn và V là thể tích của khối nón. Tính giá trị biểu thức T = l i m n → + ∞ = V 1 + V 2 + . . . + V n V
![]()
![]()
![]()
![]()
Cắt một hình nón bằng một mặt phẳng qua trục của nó được thiết diện là tam giác đểu cạnh bằng a. Tính thể tích V của khối nón theo a
Đọc tiếp
Cắt một hình nón bằng một mặt phẳng qua trục của nó được thiết diện là tam giác đểu cạnh bằng a. Tính thể tích V của khối nón theo a
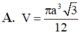
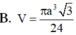
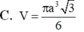
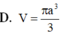
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng
a
3
. Gọi
V
1
,
V
2
lần lượt thể tích khối cầu và khối nón ngoại tiếp hình chóp S.ABCD. Tính tỷ số
V
1
V
2
A.
V
1...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng a 3 . Gọi V 1 , V 2 lần lượt thể tích khối cầu và khối nón ngoại tiếp hình chóp S.ABCD. Tính tỷ số V 1 V 2
A. V 1 V 2 = 324 25
B. V 1 V 2 = 18 30 25
C. V 1 V 2 = 36 25
D. V 1 V 2 = 108 25
Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng 8
π
Tính chiều cao của hình nón này.
Đọc tiếp
Cho hình nón có thiết diện qua trục là tam giác đều và có diện tích xung quanh bằng 8 π Tính chiều cao của hình nón này.
![]()
![]()
![]()
![]()
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các kích thước là AB 2, AD 3, AA’ 4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB’A’ và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật CDD’C’. Tính thể tích V của hình nón (N). A.
13
3
π
B. 5
π
C. 8
π
D.
25
6
π
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có các kích thước là AB= 2, AD= 3, AA’= 4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB’A’ và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật CDD’C’. Tính thể tích V của hình nón (N).
A. 13 3 π
B. 5 π
C. 8 π
D. 25 6 π
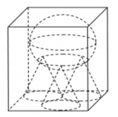
Có một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba khối nón giống nhau có thiết diện qua trục là một tam giác vuông cân vào bể sao cho ba đường tròn đáy của ba khối nón tiếp xúc với nhau, một khối nón có đường tròn đáy chỉ tiếp xúc với một cạnh của đáy bể và hai khối nón còn lại có đường tròn đáy tiếp xúc với hai cạnh của đáy bể. Sau đó người ta đặt lên đỉnh của ba khối nón một khối cầu có bán kính bằng
4
3
lần bán kính đáy của khối nón. Biết...
Đọc tiếp
Có một bể hình hộp chữ nhật chứa đầy nước. Người ta cho ba khối nón giống nhau có thiết diện qua trục là một tam giác vuông cân vào bể sao cho ba đường tròn đáy của ba khối nón tiếp xúc với nhau, một khối nón có đường tròn đáy chỉ tiếp xúc với một cạnh của đáy bể và hai khối nón còn lại có đường tròn đáy tiếp xúc với hai cạnh của đáy bể. Sau đó người ta đặt lên đỉnh của ba khối nón một khối cầu có bán kính bằng 4 3 lần bán kính đáy của khối nón. Biết khối cầu vừa đủ ngập trong nước và lượng nước trào ra là 337 π 3 c m 3 Tính thể tích nước ban đầu ở trong bể.
A. ≈ 885 , 2 c m 3
B. ≈ 1209 , 2 c m 3
C. ≈ 1106 , 2 c m 3
D. ≈ 1174 , 2 c m 3
Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài 2a. Thể tích của khối nón là
Đọc tiếp
Thiết diện qua trục của một hình nón là một tam giác đều cạnh có độ dài 2a. Thể tích của khối nón là
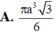
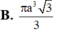
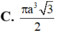
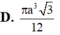
Khi cắt khối nón (N) bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác vuông cân có cạnh huyền bằng
2
a
3
Tính thể tích V của khối nón (N)
Đọc tiếp
Khi cắt khối nón (N) bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác vuông cân có cạnh huyền bằng 2 a 3 Tính thể tích V của khối nón (N)
![]()
![]()
![]()
![]()
Khi cắt khối nón (N) bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác vuông cân có cạnh huyền bằng 2 a 3 Tính thể tích V của khối nón (N).




