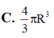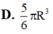Các câu hỏi tương tự
Cho tấm tôn hình nón có bán kính đáy là r
2
3
, độ dài đường sinh l 2. Người ta cắt theo một đường sinh và trải phẳng ra được một hình quạt. Gọi M, N thứ tự là trung điểm OA và OB. Hỏi khí cắt hình quạt theo hình chử nhật MNPQ (hình vẽ) và tạo thành hình trụ đường sinh PN trùng MQ (2 đáy làm riêng) thì được khối trụ có thể tích bằng bao nhiêu?
A
.
3
π
(...
Đọc tiếp
Cho tấm tôn hình nón có bán kính đáy là r = 2 3 , độ dài đường sinh l = 2. Người ta cắt theo một đường sinh và trải phẳng ra được một hình quạt. Gọi M, N thứ tự là trung điểm OA và OB. Hỏi khí cắt hình quạt theo hình chử nhật MNPQ (hình vẽ) và tạo thành hình trụ đường sinh PN trùng MQ (2 đáy làm riêng) thì được khối trụ có thể tích bằng bao nhiêu?
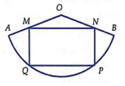
A . 3 π ( 13 - 1 ) 8
B . 3 ( 13 - 1 ) 8 π
C . 5 ( 13 - 1 ) 12 π
D . π ( 13 - 1 ) 9
Cho hình nón có chiều cao h, đường tròn đáy có bán kính R. Một mặt phẳng (P) di động song song với đáy hình nón cắt hình nón theo đường tròn giao tuyến (L) Dựng hình trụ có một đáy là đường tròn (L) một đáy nằm trên đáy hình nón có trục là trục của hình nón. Gọi x là chiều cao của hình trụ, giá trị của x để hình trụ có thể tích lớn nhất A.
x
h
2
B.
x
...
Đọc tiếp
Cho hình nón có chiều cao h, đường tròn đáy có bán kính R. Một mặt phẳng (P) di động song song với đáy hình nón cắt hình nón theo đường tròn giao tuyến (L) Dựng hình trụ có một đáy là đường tròn (L) một đáy nằm trên đáy hình nón có trục là trục của hình nón. Gọi x là chiều cao của hình trụ, giá trị của x để hình trụ có thể tích lớn nhất
A. x = h 2
B. x = h 3
C. x = h 4
D. x= h
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).
Đọc tiếp
Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của cốc nước. Người ta từ từ thả vào cốc nước viên bi và khối nón đó (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số thể tích của lượng nước còn lại trong cốc và lượng nước ban đầu (bỏ qua bề dày của lớp vỏ thủy tinh).

![]()
![]()
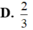
Cho hình trụ có bán kính đáy là R, độ dài đường cao là h. Đường kính MN của đáy dưới vuông góc với đường kính PQ của đáy trên. Thể tích của khối tứ diện MNPQ bằng A.
2
3
R
2
h
B.
1
6
R
2
h
C.
1
3...
Đọc tiếp
Cho hình trụ có bán kính đáy là R, độ dài đường cao là h. Đường kính MN của đáy dưới vuông góc với đường kính PQ của đáy trên. Thể tích của khối tứ diện MNPQ bằng
A. 2 3 R 2 h
B. 1 6 R 2 h
C. 1 3 R 2 h
D. 2 R 2 h
Cho hình chóp nón N có bán kính đáy bằng R, đường cao SO. Một mặt phẳng (P) cố định vuông góc với SO tại O’ và cắt khối nón theo hình nón có bán kính R’. Mặt phẳng (Q) thay đổi, vuông góc với SO tại điểm
O
1
(
O
1
nằm giữa O và O) cắt khối nón theo thiết diện là hình tròn có bán kính x.Tính xtheo R và R’ để (Q) chia phần khối nón nằm giữa (P) và đáy hình nón thành hai phần có thể tích...
Đọc tiếp
Cho hình chóp nón N có bán kính đáy bằng R, đường cao SO. Một mặt phẳng (P) cố định vuông góc với SO tại O’ và cắt khối nón theo hình nón có bán kính R’. Mặt phẳng (Q) thay đổi, vuông góc với SO tại điểm O 1 ( O 1 nằm giữa O và O') cắt khối nón theo thiết diện là hình tròn có bán kính x.Tính xtheo R và R’ để (Q) chia phần khối nón nằm giữa (P) và đáy hình nón thành hai phần có thể tích bằng nhau
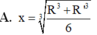
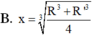
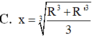
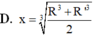
Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón (N). Diện tích toàn phần
S
t
p
của hình nón (N) bằng
Đọc tiếp
Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón (N). Diện tích toàn phần S t p của hình nón (N) bằng
![]()
![]()
![]()
![]()
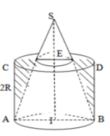
Xét một hình trụ nội tiếp trong hình nón như hình bên, trong đó S là đỉnh hình nón, O là tâm đường tròn mặt đáy. Các đoạn AB, CD lần lượt là đường kính của đường tròn đáy của hình nón và hình trụ. Biết AC, BD cắt nhau tại điểm M (M
∈
SO) tỉ số thể tích của hình trụ và hình nón là
4
9
. Tính tỉ số
S
M
S...
Đọc tiếp
Xét một hình trụ nội tiếp trong hình nón như hình bên, trong đó S là đỉnh hình nón, O là tâm đường tròn mặt đáy. Các đoạn AB, CD lần lượt là đường kính của đường tròn đáy của hình nón và hình trụ. Biết AC, BD cắt nhau tại điểm M (M ∈ SO) tỉ số thể tích của hình trụ và hình nón là 4 9 . Tính tỉ số S M S O

A. 7 9
B. 2 3
C. 4 5
D. 5 6
Cho hình trụ có hai đáy là hai hình tròn (O) và (O), chiều cao bằng 2R và bán kính đáy R. mặt phẳng (P) đi qua trung điểm của (OO) và tạo với OO một góc
30
o
cắt đường tròn dáy theo dây cung . Tính độ dài day cung đó theo R
Đọc tiếp
Cho hình trụ có hai đáy là hai hình tròn (O) và (O'), chiều cao bằng 2R và bán kính đáy R. mặt phẳng (P) đi qua trung điểm của (OO') và tạo với OO' một góc 30 o cắt đường tròn dáy theo dây cung . Tính độ dài day cung đó theo R
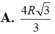
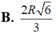
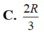
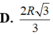
Hình trụ có bán kính đáy r. Gọi O và O là tâm của hai đường tròn đáy, với OO’ 2r .Một mặt cầu (S ) tiếp xúc với hai đáy hình trụ tại O và O. Gọi VC và VT lần lượt là thể tích khối cầu và khối trụ tương ứng. Khi đó
V
C
V
T
bằng: A.
1
2
B.
3
4
C.
2...
Đọc tiếp
Hình trụ có bán kính đáy r. Gọi O và O' là tâm của hai đường tròn đáy, với OO’ = 2r .Một mặt cầu (S ) tiếp xúc với hai đáy hình trụ tại O và O'. Gọi VC và VT lần lượt là thể tích khối cầu và khối trụ tương ứng. Khi đó V C V T bằng:
A. 1 2
B. 3 4
C. 2 3
D. 3 5