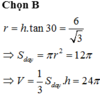Các câu hỏi tương tự
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là
β
. Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng. A.
2
R
3
π
9
tan
β...
Đọc tiếp
Một hình nón có bán kính đáy là R, góc giữa đường cao và một đường sinh là β . Biết rằng đường chéo thiết diện qua trục hình trụ thì song song với đường sinh hình nón. Thể tích của khối trụ nội tiếp hình nón bằng.
A. 2 R 3 π 9 tan β
B. 4 R 3 π 27 tan β
C. 2 R 3 π 27 tan β
D. 2 R 3 π 3 tan β
Cho hình nón có chiều cao bằng 2 và đường sinh hợp với trục một góc bằng
45
O
. Diện tích xung quanh của hình nón là: A.
4
3
π
B.
2
π
C.
3
π
D.
4
2...
Đọc tiếp
Cho hình nón có chiều cao bằng 2 và đường sinh hợp với trục một góc bằng 45 O . Diện tích xung quanh của hình nón là:
A. 4 3 π
B. 2 π
C. 3 π
D. 4 2 π
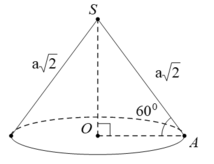
Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a
2
và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh
S
xq
của hình nón và thể tích V của khối nón tương ứng là: A.
S
xq
πa
2
;
V
πa...
Đọc tiếp
Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a 2 và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh S xq của hình nón và thể tích V của khối nón tương ứng là:
A. S xq = πa 2 ; V = πa 3 6 12
B. S xq = πa 2 2 ; V = πa 3 3 12
C. S xq = πa 2 2 ; V = πa 3 6 4
D. S xq = πa 2 ; V = πa 3 6 4
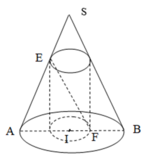
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng
α
. Gọi I là một điểm trên đường cao DO của hình nón sao cho
DI
DO
k (0 k 1) . Tính diện tích thiết diện qua I và vuông góc với trục của hình nón.
Đọc tiếp
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng α . Gọi I là một điểm trên đường cao DO của hình nón sao cho DI DO = k (0 < k < 1) . Tính diện tích thiết diện qua I và vuông góc với trục của hình nón.
Cho khối nón có chiều cao bằng a và thể tích bằng
4
πa
3
3
độ dài đường sinh của hình nón bằng
Đọc tiếp
Cho khối nón có chiều cao bằng a và thể tích bằng 4 πa 3 3 độ dài đường sinh của hình nón bằng
![]()
![]()
![]()

Cho khối nón có độ dài đường sinh bằng 2a, góc giữa đường sinh và đáy bằng 60°. Thể tích của khối nón đã cho là
Đọc tiếp
Cho khối nón có độ dài đường sinh bằng 2a, góc giữa đường sinh và đáy bằng 60°. Thể tích của khối nón đã cho là
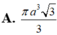
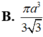
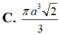
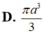
Một hình nón có đường sinh bằng
a
2
và góc giữa đường sinh và mặt phẳng đáy bằng
60
°
. Tính thể tích của khối nón được tạo nên từ hình nón đó.
Đọc tiếp
Một hình nón có đường sinh bằng a 2 và góc giữa đường sinh và mặt phẳng đáy bằng 60 ° . Tính thể tích của khối nón được tạo nên từ hình nón đó.
![]()
![]()
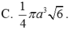
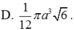
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng α . Tính diện tích xung quanh của hình nón và thể tích khối nón được tạo nên.
II. Tự luận ( 4 điểm)
Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a 2 và góc giữa đường sinh và mặt phẳng đáy bằng 60°. Diện tích xung quanh S x q của hình nón và thể tích V của khối nón tương ứng là: