Tâm mặt cầu tiếp xúc 6 mặt của hình lập phương là trung điểm O của EE’
Bán kính mặt cầu là OE = 1/2 EE’ = 1/2 AA’ = 1/2 a
Tâm mặt cầu tiếp xúc 6 mặt của hình lập phương là trung điểm O của EE’
Bán kính mặt cầu là OE = 1/2 EE’ = 1/2 AA’ = 1/2 a
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Hãy xác định tâm và bán kính mặt cầu:
Đi qua 8 đỉnh của hình lập phương.
Cho mặt nón có chiều cao h = 6, bán kính đáy r = 3. Hình lập phương ABCD.A’B’C’D’ đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong cùng một mặt phẳng đáy của hình trụ, các đỉnh của đáy còn lại thuộc các đường sinh của hình nón. Độ dài đường chéo của hình lập phương bằng
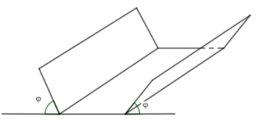
A. 3 3
B. 3 6 2
C. 6 3 2 - 1
D. 6 2 - 1
Cho mặt nón có chiều cao h = 6 bán kính đáy r = 3. Một hình lập phương đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong mặt đáy của hình nón, các đỉnh còn lại thuộc các đường sinh của hình nón. Tính độ dài cạnh của hình lập phương.
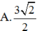
![]()
![]()
![]()
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Bán kính mặt cầu ngoại tiếp hình lập phương là:
A. a
B. a 2 2
C. a 3 2
D. a 2
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Mặt phẳng (P) đi qua đường chéo BD’ cắt các cạnh CD, A'B' và tạo với hình lập phương một thiết diện, khi diện tích thiết diện đạt giá trị nhỏ nhất, cosin góc tạo bởi (P) và mặt phẳng (ABCD) bằng
A. 10 4
B. 6 3
C. 6 6
D. 3 3
Một khối đa diện được tạo thành bằng cách từ một khối lập phương cạnh bằng 3, ta bỏ đi khối lập phương cạnh bằng 1 ở một “góc” của nó như hình vẽ.
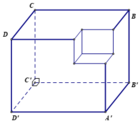
Gọi S là khối cầu có thể tích lớn nhất chứa trong H và tiếp xúc với các mặt phẳng (A'B'C'D'), (BCC'B') và (DCC'D'). Tính bán kính của S.
A . 2 + 3 3
B . 3 - 3
C . 2 3 3
D . 2
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính diện tích mặt cầu đi qua tất cả các đỉnh của hình lập phương.
Tính bán kính R của mặt cầu ngoại tiếp một hình lập phương có cạnh bằng a.
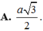
![]()
![]()
![]()
Tính bán kính R của mặt cầu ngoại tiếp một hình lập phương có cạnh bằng a.
![]()
![]()
![]()
![]()