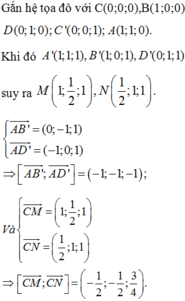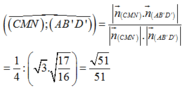Các câu hỏi tương tự
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Mặt phẳng (P) đi qua đường chéo BD’ cắt các cạnh CD, A’B’ và tạo với hình lập phương một thiết diện, khi diện tích thiết diện đạt giá trị nhỏ nhất, cosin góc tạo bởi (P) và mặt phẳng (ABCD) bằng A.
10
4
B.
6
3
C.
6
6
D.
3
3
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 2. Mặt phẳng (P) đi qua đường chéo BD’ cắt các cạnh CD, A’B’ và tạo với hình lập phương một thiết diện, khi diện tích thiết diện đạt giá trị nhỏ nhất, cosin góc tạo bởi (P) và mặt phẳng (ABCD) bằng
A. 10 4
B. 6 3
C. 6 6
D. 3 3
Cho hình lăng trụ tam giác đều ABC.ABC có
A
B
2
3
,
A
A
2
. Gọi M, N, P lần lượt là trung điểm của các cạnh AB,AC và BC (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng ( ABC ) và ( MNP ) bằng A.
6
13
65
B.
13...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' có A B = 2 3 , A A ' = 2 . Gọi M, N, P lần lượt là trung điểm của các cạnh A'B',A'C' và BC (tham khảo hình vẽ bên). Côsin của góc tạo bởi hai mặt phẳng ( AB'C' ) và ( MNP ) bằng

A. 6 13 65
B. 13 65
C. 17 13 65
D. 18 13 65
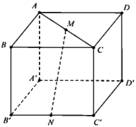
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng A.
5
a
B.
5
a
5
.
C. 3a D.
a
3
.
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
A. 5 a
B. 5 a 5 .
C. 3a
D. a 3 .
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng A.
5
a
B.
5
a
5
C. 3a D. a/3
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng

A. 5 a
B. 5 a 5
C. 3a
D. a/3
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có
A
B
2
3
và AA’2. Gọi M và N lần lượt là trung điểm của A’C’ và A’B’ (như hình vẽ bên). Tính cosin của góc tạo bởi hai mặt phẳng (AB’C’) và (BCMN). A.
13
65
B.
13
130
C.
-
13
130
D.
-...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có A B = 2 3 và AA’=2. Gọi M và N lần lượt là trung điểm của A’C’ và A’B’ (như hình vẽ bên). Tính cosin của góc tạo bởi hai mặt phẳng (AB’C’) và (BCMN).
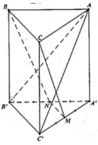
A. 13 65
B. 13 130
C. - 13 130
D. - 13 65
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có
A
B
2
3
và AA’2. Gọi M,N,P lần lượt là trung điểm của các cạnh A’B’, A’C’ và BC. Côsin của góc tạo bởi hai mặt phẳng (AB’C’) và (MNP) bằng A.
6
13
65
B.
13
65
.
C.
17
13...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có A B = 2 3 và AA’=2. Gọi M,N,P lần lượt là trung điểm của các cạnh A’B’, A’C’ và BC. Côsin của góc tạo bởi hai mặt phẳng (AB’C’) và (MNP) bằng
A. 6 13 65
B. 13 65 .
C. 17 13 65 .
D. 18 63 65 .
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M,N lần lượt là trung điểm của các cạnh A’B’ và BC. Mặt phẳng (DMN) chia hình lập phương thành 2 phần. Gọi V1 là thể tích của phần chứa đỉnh A, V2 là thể tích của phần còn lại. Tính tỷ số
V
1
V
2
A. 2/3 B. 55/89 C. 37/48 D. 1/2
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M,N lần lượt là trung điểm của các cạnh A’B’ và BC. Mặt phẳng (DMN) chia hình lập phương thành 2 phần. Gọi V1 là thể tích của phần chứa đỉnh A, V2 là thể tích của phần còn lại. Tính tỷ số V 1 V 2
A. 2/3
B. 55/89
C. 37/48
D. 1/2
Cho hình lập phương
A
B
C
D
.
A
1
B
1
C
1
D
1
có cạnh bằng 1. Hai điểm M, N lần lượt thay đổi trên các đoạn
A
B
1
và
B
C
1
sao cho MN luôn tạo với mặt phẳng (ABCD) một góc
60...
Đọc tiếp
Cho hình lập phương A B C D . A 1 B 1 C 1 D 1 có cạnh bằng 1. Hai điểm M, N lần lượt thay đổi trên các đoạn A B 1 và B C 1 sao cho MN luôn tạo với mặt phẳng (ABCD) một góc 60 0 (tham khảo hình vẽ). Giá trị bé nhất của đoạn MN là

A. 3 3
B. 2 2 − 1
C. 2 3 − 2
D. 3 − 1
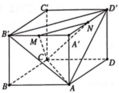
Trong không gian Oxyz, cho hình lập phương ABCD.ABCD có tọa độ các đỉnh A(0;0;0),B(1;0;0), D(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADDA. Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng A.
3
5
4
14
B.
14...
Đọc tiếp
Trong không gian Oxyz, cho hình lập phương ABCD.A'B'C'D' có tọa độ các đỉnh A(0;0;0),B(1;0;0), D(0;1;0) và A’(0;0;1). Gọi M là trung điểm cạnh AB và N là tâm của hình vuông ADD'A'. Diện tích của thiết diện tạo bởi mặt phẳng (CMN) và hình lập phương đã cho bằng
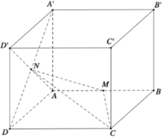
A. 3 5 4 14
B. 14 4
C. 3 14 4 5
D. 9 4 14