Đáp án C
Ta có: S N A D = 1 2 d N ; A D . A D = 1 2 a 2
d M ; A B C D = A A ' = a
Do đó V M . A D N = 1 3 . A A ' . S N A D = a 3 6 .
Đáp án C

Ta có: S N A D = 1 2 d N ; A D . A D = 1 2 a 2
d M ; A B C D = A A ' = a
Do đó V M . A D N = 1 3 . A A ' . S N A D = a 3 6 .
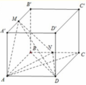
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a . Gọi O và O' lần lượt là tâm các hình vuông. Gọi Mvà N lần lượt là trung điểm của các cạnh B' C' và CD. Tính thể tích khối tứ diện OO'MN.
A. a 3 8
B. a 3
C. a 3 12
D. a 3 24
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a. Gọi M, N lần lượt nằm trên các cạnh A ' B ' và BC sao cho M A ' = M B ' và NB = 2NC. Mặt phẳng (DMN) chia khối lập phương đã cho thành hai khối đa diện. Gọi V H là thể tích khối đa diện chứa đỉnh A, V ( H ' ) là thể tích khối đa diện còn lại. Tỉ số V H V H ' bằng
A. 151 209
B. 209 360
C. 2348 3277
D. 151 360
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 8
D. 13 2 a 3 216
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, BC và E là điểm đối xứng với B qua D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối chứa điểm A có thể tích V. Tính V.
A. 11 2 a 3 216
B. 7 2 a 3 216
C. 2 a 3 18
D. 13 2 a 3 216
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Gọi M, N lần lượt là trung điểm của cạnh A ' B ' và BC. Mặt phẳng (DMN) chia khối lập phương thành hai khối đa diện. Gọi (H) là khối đa diện chứa đỉnh A và H ' là khối đa diện còn lại. Tính tỉ số V H V H '
A. V H V H ' = 55 89
B. V H V H ' = 37 48
C. V H V H ' = 1 2
D. V H V H ' = 2 3
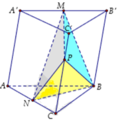
Cho hình lăng trụ ABC.A'B'C' có thể tích bằng V. Gọi M, N lần lượt là trung điểm của A'B', AC và P là điểm thuộc cạnh CC' sao cho CP=2C'P (như hình vẽ). Tính thể tích khối tứ diện BMNP theo V
A. V 3
B. 2 V 9
C. 4 V 9
D. 5 V 24
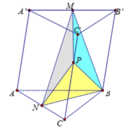
Cho hình lăng trụ ABC.A'B'C' có thể tích bằng V. Gọi M, N lần lượt là trung điểm của A'B', AC và P là điểm thuộc cạnh CC' sao cho CP=2C'P (như hình vẽ). Tính thể tích khối tứ diện BMNP theo V.
A. V 3
B. 2 V 9
C. 4 V 9
D. 5 V 24
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , S A = a và S A ⊥ A B C D . Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho S N = 2 S D . Tính thể tích V của khối tứ diện ACMN
A. V = a 3 8
B. V = a 3 36
C. V = a 3 6
D. V = a 3 12
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=a và SA vuông góc với đáy. Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho SN=2ND. Tính thể tích V của khối tứ diện ACMN.
A. V = 1 12 a 3
B. V = 1 6 a 3
C. V = 1 8 a 3
D. V = 1 36 a 3