Các câu hỏi tương tự
AB là đoạn vuông góc chung của 2 đường thẳng
∆
,
∆
chéo nhau,
A
∈
∆
,
B
∈
∆
,
A
B
a
;
M
là điểm di động trên
∆
,
N
là điểm di động trên
∆
. Đặt
A
M
m
,
...
Đọc tiếp
AB là đoạn vuông góc chung của 2 đường thẳng ∆ , ∆ ' chéo nhau, A ∈ ∆ , B ∈ ∆ ' , A B = a ; M là điểm di động trên ∆ , N là điểm di động trên ∆ ' . Đặt A M = m , A N = n m ≥ 0 , n ≥ 0 . Giả sử ta luôn có m 2 + n 2 = b với b > 0 không đổi. Xác định m, n để độ dài đoạn MN đạt giá trị lớn nhất.
A. m = n = a b 2
B. m = n = b 2
C. m = a 2 ; n = b 2
D. m = a b 2 ; n = a + b 2
Cho hình lập phương
A
B
C
D
.
A
B
C
D
cạnh bằng a. Lấy điểm M thuộc đoạn AD¢, điểm N thuộc đoạn BD sao cho
A
M
D
N
x
với
0
x
a
2...
Đọc tiếp
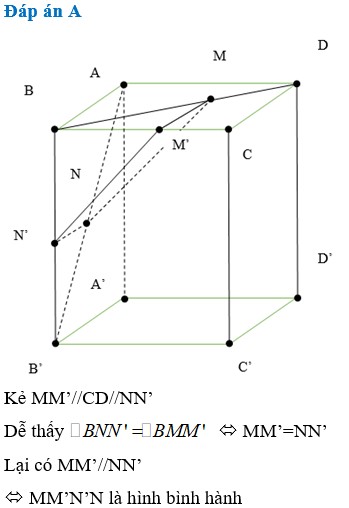
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh bằng a. Lấy điểm M thuộc đoạn AD¢, điểm N thuộc đoạn BD sao cho A M = D N = x với 0 < x < a 2 2 . Tìm x theo a để đoạn MN ngắn nhất
A. x = a 2 3
B. x = a 2 4
C. x = a 2
D. 0
AB là đoạn vuông góc chung của 2 đường thẳng
∆
,
∆
chéo nhau,
A
B
∈
∆
,
B
∈
∆
,
A
B
a
M là điểm di động trên
∆
, N là điểm di động trên
∆
. Đặt AMm, ANn
m
,
n
≥
0
. Giả sử ta luôn có
m...
Đọc tiếp
AB là đoạn vuông góc chung của 2 đường thẳng ∆ , ∆ ' chéo nhau, A B ∈ ∆ , B ∈ ∆ ' , A B = a M là điểm di động trên ∆ , N là điểm di động trên ∆ ' . Đặt AM=m, AN=n m , n ≥ 0 . Giả sử ta luôn có m 2 + n 2 = b với b>0, b không đổi. Xác định m, n để độ dài đoạn MN đạt giá trị lớn nhất
A. m = n = a b 2
B. m = n = b 2
C. m = a 2 , n = b 2
D. m = a b 2 , n = a + b 2
Cho hình trụ
T
có chiều cao bằng đường kính đáy, hai đáy là các hình tròn
O
;
r
và
O
;
r
. Gọi A là điểm di động trên đường tròn
O
;
r
v à B là điểm di động trên đường tròn
O
;
r...
Đọc tiếp
Cho hình trụ T có chiều cao bằng đường kính đáy, hai đáy là các hình tròn O ; r và O ' ; r . Gọi A là điểm di động trên đường tròn O ; r v à B là điểm di động trên đường tròn O ' ; r sao cho AB không là đường sinh của hình trụ T . Khi thể tích khối tứ diện O O ' A B đạt giá trị lớn nhất thì đoạn thẳng AB có độ dài bằng
A. 3 r
B. 2 + 2 r
C. 6 r
D. 5 r
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;0;2),B(0;2;-2). Các điểm M, N lần lượt di động trên các đoạn thẳng OA, OB sao cho MN chia tam giác OAB thành hai phần có diện tích bằng nhau. Khi MN ngắn nhất thì toạ độ trọng tâm của tam giác OMN là A. (
2
4
;
2
4
; 0) B. (
2
3
;
2...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;0;2),B(0;2;-2). Các điểm M, N lần lượt di động trên các đoạn thẳng OA, OB sao cho MN chia tam giác OAB thành hai phần có diện tích bằng nhau. Khi MN ngắn nhất thì toạ độ trọng tâm của tam giác OMN là
A. ( 2 4 ; 2 4 ; 0)
B. ( 2 3 ; 2 3 ; 0)
C. ( 1 3 ; 1 3 ; 0)
D. ( 1 4 ; 1 4 ; 0)
Trong không gian Oxyz, cho đường thẳng
d
:
x
4
-
3
t
y
3
+
4
t
z...
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng d : x = 4 - 3 t y = 3 + 4 t z = 0 . Gọi A là hình chiếu vuông góc của O trên d. Điểm M di động trên tia Oz, điểm N di động trên đường thẳng d sao cho MN = OM + AN. Gọi I là trung điểm của đoạn thẳng OA. Trong trường hợp diện tích tam giác IMN đạt giá trị nhỏ nhất, một vectơ pháp tuyến của mặt phẳng (M, d) có tọa độ là
A. 4 ; 3 ; 5 2
B. 4 ; 3 ; 10 2
C. 4 ; 3 ; 5 10
D. 4 ; 3 ; 10 10
Cho hình lập phương ABCDABCD có cạnh bằng a. Điểm M thuộc đoạn thẳngBC, điểm N thuộc đoạn thẳng AB,MN tạo với mặt phẳng đáy một góc
30
°
. Tìm độ dài nhỏ nhất của đoạn thẳng MN. A.
a
2
B.
2
a
3
C.
2
a
5
−
1
D....
Đọc tiếp
Cho hình lập phương ABCDA'B'C'D' có cạnh bằng a. Điểm M thuộc đoạn thẳngBC', điểm N thuộc đoạn thẳng AB',MN tạo với mặt phẳng đáy một góc 30 ° . Tìm độ dài nhỏ nhất của đoạn thẳng MN.
A. a 2
B. 2 a 3
C. 2 a 5 − 1
D. 2 a 5 + 1
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x+2y-z+160 và mặt cầu (s): (x-2)2 + (y+1)2 + (z-3)29. Điểm M di động trên trên (S) và điểm N di động trên (P) sao cho độ dài đoạn thẳng MN ngắn nhất. Tọa độ điểm M là A. M(0;1;-1) B. M(0;-3;4) C. M(2;0;1) D. M(-2;2;-3)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x+2y-z+16=0 và mặt cầu (s): (x-2)2 + (y+1)2 + (z-3)2=9. Điểm M di động trên trên (S) và điểm N di động trên (P) sao cho độ dài đoạn thẳng MN ngắn nhất. Tọa độ điểm M là
A. M(0;1;-1)
B. M(0;-3;4)
C. M(2;0;1)
D. M(-2;2;-3)
Cho hình lập phương
ABCD
.
A
B
C
D
có cạnh bằng a. Một đường thẳng d đi qua đỉnh D¢ và tâm I của mặt bên
BCC
B
.
Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng
BCC
B
và
ABCD
sao cho trung điểm K của MN thuộc đường thẳn...
Đọc tiếp
Cho hình lập phương ABCD . A ' B ' C ' D ' có cạnh bằng a. Một đường thẳng d đi qua đỉnh D¢ và tâm I của mặt bên BCC ' B ' . Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng BCC ' B ' và ABCD sao cho trung điểm K của MN thuộc đường thẳng d (tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là
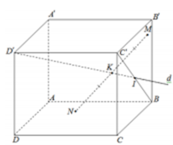
A. 3 a 2
B. 3 5 a 10
C. 2 5 a 5
D. 2 3 a 5