Các câu hỏi tương tự
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A′B′C′D′. A.
S
πa
2
2
2
B.
S
2
πa
2
C.
S
π
2...
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A′B′C′D′.
A. S = πa 2 2 2
B. S = 2 πa 2
C. S = π 2 a 2
D. S = πa 2
Cho hình lập phương ABCD.A′B′C′D′. Gọi O,O′ lần lượt là tâm của hai hình vuông ABCD và A′B′C′D′. Gọi
V
1
là thể tích của khối trụ tròn xoay có đáy là 2 đường tròn ngoại tiếp hình vuông ABCD và A′B′C′D′,
V
2
là thể tích khối nón tròn xoay đỉnh O và có đáy là đường tròn nội tiếp hình vuông A′B′C′D′. Tỷ số thể tích
V
1
V
2...
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′. Gọi O,O′ lần lượt là tâm của hai hình vuông ABCD và A′B′C′D′. Gọi V 1 là thể tích của khối trụ tròn xoay có đáy là 2 đường tròn ngoại tiếp hình vuông ABCD và A′B′C′D′, V 2 là thể tích khối nón tròn xoay đỉnh O và có đáy là đường tròn nội tiếp hình vuông A′B′C′D′. Tỷ số thể tích V 1 V 2 là
A. 6
B. 2
C. 8
D. 4
Cho hai điểm A, B thuộc đồ thị hàm số y sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD 2 π /3. Độ dài của cạnh BC bằng A.
2
2
B.
1
2
C. 1 D.
3
2
Đọc tiếp
Cho hai điểm A, B thuộc đồ thị hàm số y = sinx trên đoạn [0;π], các điểm C, D thuộc trục Ox thỏa mãn ABCD là hình chữ nhật và CD = 2 π /3. Độ dài của cạnh BC bằng
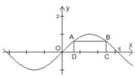
A. 2 2
B. 1 2
C. 1
D. 3 2
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khối nón đỉnh A, đáy là đường tròn đi qua ba điểm A′BD có thể tích bằng A.
2
3
πa
3
27
B.
3
πa
3
8
C. ...
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khối nón đỉnh A, đáy là đường tròn đi qua ba điểm A′BD có thể tích bằng
A. 2 3 πa 3 27
B. 3 πa 3 8
C. 3 a 3 27
D. πa 3 6
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB,C′D′ bằng
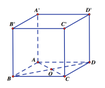
A. 2 a
B. a
C. 3 a
D. 3 2 a
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB,C′D′ bằng A.
2
a
B.
a
C.
3
a
D.
a
3
2
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Khoảng cách giữa hai đường thẳng AB,C′D′ bằng

A. 2 a
B. a
C. 3 a
D. a 3 2
Phương trình sin 3 x 3 = sin 5 x 5 có 3 nghiệm phân biệt A, B, C thuộc nửa khoảng [ 0 ; π ] khi đó cosA+cosB+cosC bằng
A. 1
B. 1/3
C. -4/3
D. 0
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách từ điểm A đến mặt phẳng (A′B′CD) bằng A.
a
2
B.
3
a
C.
3
3
a
D.
2
2
a
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách từ điểm A đến mặt phẳng (A′B′CD) bằng
A. a 2
B. 3 a
C. 3 3 a
D. 2 2 a
Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy là hình vuông cạnh bằng 4cm, đường chéo AB′ của mặt bên (ABB′A′) có độ dài bằng 5cm. Tính thể tích V của khối lăng trụ ABCD.A′B′C′D′. A.
48
cm
3
B.
24
cm
3
C.
16
cm
3
D.
32
cm
3
Đọc tiếp
Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy là hình vuông cạnh bằng 4cm, đường chéo AB′ của mặt bên (ABB′A′) có độ dài bằng 5cm. Tính thể tích V của khối lăng trụ ABCD.A′B′C′D′.
A. 48 cm 3
B. 24 cm 3
C. 16 cm 3
D. 32 cm 3
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách giữa hai đường thẳng BD và A′C′ bằng A.
2
a. B. a. C.
3
a. D.
2
a
2
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ cạnh a. Khoảng cách giữa hai đường thẳng BD và A′C′ bằng
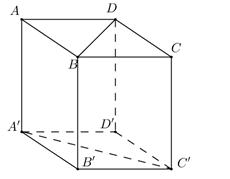
A. 2 a.
B. a.
C. 3 a.
D. 2 a 2




