Question

Cho hình lăng trụ tam giác ABC .A'B'C'. Gọi M, N lần lượt là trung điểm của AB, AC. Gọi O là giao điểm của AB' và A'B. Chứng minh rằng

a) vecto MN =1/2 vecto B'C'

b) vecto CC' = (-2)vecto OM

Answer 1

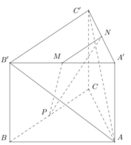
a: Xét ΔABC có M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC

=>MN//BC và \(MN=\frac12BC\)

=>\(\overrightarrow{MN}=\frac12\cdot\overrightarrow{BC}\)

mà \(\overrightarrow{BC}=\overrightarrow{B^{\prime}C^{\prime}}\) (BCC'B' là hình bình hành)

nên \(\overrightarrow{MN}=\frac12\cdot\overrightarrow{B^{\prime}C^{\prime}}\)

b: Vì ABC.A'B'C' là lăng trụ đứng nên AA'//BB' và AA'=BB'

=>A'ABB' là hình bình hành

=>AB' cắt A'B tại trung điểm của mỗi đường

=>O là trung điểm chung của AB' và A'B

Xét ΔABB' có

O,M lần lượt là trung điểm của AB',AB

=>OM là đường trung bình của ΔABB'

=>OM//B'B và \(OM=\frac12B^{\prime}B\)

=>\(\overrightarrow{OM}=\frac12\cdot\overrightarrow{B^{\prime}B}=-\frac12\cdot\overrightarrow{BB^{\prime}}\)

=>\(\overrightarrow{OM}=-\frac12\cdot\overrightarrow{C^{}C^{\prime}}\)

=>\(\overrightarrow{CC^{\prime}}=-2\cdot\overrightarrow{OM}\)