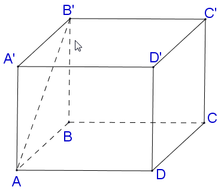
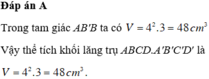Các câu hỏi tương tự
Cho hình trụ lăng đứng đáy là tam giác vuông có một cạnh góc vuông bằng 3 cm, cạnh huyền bằng 5 cm. Thể tích lăng trụ đó bằng 72cm3. Tính chiều cao của hình lăng trụ đó
Nếu khối lăng trụ đứng có đáy là hình vuông cạnh 2a và đường chéo mặt bên bằng 4a thì khối lăng trụ đó có thể tích bằng:` A.
4
a
3
B.
6
3
a
3
C.
8
3
a
3
D.
12
a
3
Đọc tiếp
Nếu khối lăng trụ đứng có đáy là hình vuông cạnh 2a và đường chéo mặt bên bằng 4a thì khối lăng trụ đó có thể tích bằng:`
A. 4 a 3
B. 6 3 a 3
C. 8 3 a 3
D. 12 a 3
Cho khối lăng trụ tam giác ABC.A′B′C′ có đáy là tam giác vuông tại A, AB 1,BC 2. Góc
∠
C
B
B
90
°
,
∠
A
B
B
120
°
. Gọi M là trung điểm cạnh AA′. Biết
d
A
B
,
C
M
7...
Đọc tiếp
Cho khối lăng trụ tam giác ABC.A′B′C′ có đáy là tam giác vuông tại A, AB =1,BC = 2. Góc ∠ C B B ' = 90 ° , ∠ A B B ' = 120 ° . Gọi M là trung điểm cạnh AA′. Biết d A B ' , C M = 7 7 . Tính thể tích khối lăng trụ đã cho.
A. 2 2
B. 4 2 9
C. 4 2
D. 4 2 3
Cho khối lăng trụ tứ giác đều ABCD. A B C D có khoảng cách giữa AB và A’D bằng 2, đường chéo của mặt bên bằng 5. Biết
A
A
A
D
. Thể tích lăng trụ là A.
V
30
5
B.
V
10
5...
Đọc tiếp
Cho khối lăng trụ tứ giác đều ABCD. A 'B 'C 'D ' có khoảng cách giữa AB và A’D bằng 2, đường chéo của mặt bên bằng 5. Biết A ' A > A D . Thể tích lăng trụ là
A. V = 30 5
B. V = 10 5 3
C. 10 5
D. 5 5
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A′B′C′D′. A.
S
πa
2
2
2
B.
S
2
πa
2
C.
S
π
2...
Đọc tiếp
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A′B′C′D′.
A. S = πa 2 2 2
B. S = 2 πa 2
C. S = π 2 a 2
D. S = πa 2
Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A′ xuống mặt phẳng ABC trùng với trung điểm của cạnh AB. Mặt bên (ACC′A′) tạo với đáy một góc
60
0
. Tính thể tích khối lăng trụ ABC.A′B′C′. A.
3
a
3
2
B.
3
a...
Đọc tiếp
Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A′ xuống mặt phẳng ABC trùng với trung điểm của cạnh AB. Mặt bên (ACC′A′) tạo với đáy một góc 60 0 . Tính thể tích khối lăng trụ ABC.A′B′C′.
A. 3 a 3 2
B. 3 a 3 3 2
C. a 3 3 2
D. a 3 3 3
Cho hình lăng trụ đứng
A
B
C
.
A
B
C
có đáy ABC là tam giác vuông cân tại A, mặt bên
B
C
C
B
là hình vuông cạnh 2a. Thể tích của khối lăng trụ bằng A.
a
3
B.
a
3
2
C....
Đọc tiếp
Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy ABC là tam giác vuông cân tại A, mặt bên B C C ' B ' là hình vuông cạnh 2a. Thể tích của khối lăng trụ bằng
A. a 3
B. a 3 2
C. 2 a 3 3
D. 2 a 3
Cho hình lăng trụ ABCD.ABCD có đáy là hình thoi cạnh bằng a và
A
B
C
⏜
120
°
. Góc giữa cạnh bên AA và mặt đáy bằng
60
°
, điếm A’ cách đều các điểm A, B, D . Tính thể tích khối lăng trụ đã cho theo a. A.
a
3
3
3...
Đọc tiếp
Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình thoi cạnh bằng a và A B C ⏜ = 120 ° . Góc giữa cạnh bên AA' và mặt đáy bằng 60 ° , điếm A’ cách đều các điểm A, B, D . Tính thể tích khối lăng trụ đã cho theo a.
A. a 3 3 3
B. a 3 3 2
C. a 3 3 12
D. a 3 3 6
Cho hình lăng trụ đứng ABCABC có đáy ABC là tam giác vuông cân tại A, mặt bên BCCB là hình vuông cạnh 2a. Tính thể tích V của khối lăng trụ A.
V
a
3
B.
V
a
3
2
C.
V
2
a
3
3
D.
V
2...
Đọc tiếp
Cho hình lăng trụ đứng ABCA'B'C' có đáy ABC là tam giác vuông cân tại A, mặt bên BCC'B' là hình vuông cạnh 2a. Tính thể tích V của khối lăng trụ
A. V = a 3
B. V = a 3 2
C. V = 2 a 3 3
D. V = 2 a 3