Các câu hỏi tương tự
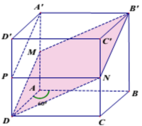
Cho hình lăng trụ đều ABCD.ABCD có đáy là hình vuông cạnh a. Mặt phẳng
α
lần lượt cắt các cạnh bên AA’, BB’, CC’ tại 4 điểm M, N, P, Q. Góc giữa mặt phẳng
α
và mặt phẳng (ABCD) là
60
0
. Diện tích tứ giác MNPQ là :
Đọc tiếp
Cho hình lăng trụ đều ABCD.A'B'C'D' có đáy là hình vuông cạnh a. Mặt phẳng α lần lượt cắt các cạnh bên AA’, BB’, CC’ tại 4 điểm M, N, P, Q. Góc giữa mặt phẳng α và mặt phẳng (ABCD) là 60 0 . Diện tích tứ giác MNPQ là :
![]()
![]()
![]()
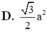
Tính theo a thể tích của khối lăng trụ đứng ABCD.ABCD có đáy là hình thoi cạnh a,
B
A
D
^
60
°
và cạnh bên AAa. A.
9
2
a
3
B.
1
2
a
3
C.
3
2
a
3
D....
Đọc tiếp
Tính theo a thể tích của khối lăng trụ đứng ABCD.A'B'C'D' có đáy là hình thoi cạnh a, B A D ^ = 60 ° và cạnh bên AA'=a.
A. 9 2 a 3
B. 1 2 a 3
C. 3 2 a 3
D. 3 2 a 3
Cho hình lăng trụ ABC.ABC có đáy là tam giác đều cạnh a,
A
A
3
a
2
. Biết rằng hình chiếu vuông góc của điểm A lên mặt phẳng (ABC) là trung điểm của cạnh BC. Tính thể tích V của khối lăng trụ đó theo a.
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a, A A ' = 3 a 2 . Biết rằng hình chiếu vuông góc của điểm A' lên mặt phẳng (ABC) là trung điểm của cạnh BC. Tính thể tích V của khối lăng trụ đó theo a.
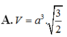
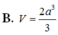
![]()
Cho hình hộp chữ nhật ABCD. ABCD có đáy ABCD là hình vuông cạnh a, AAb. Gọi M là trung điểm của cạnh CC. Tính theo a và b thể tích V của khối tứ diện BDAM
Đọc tiếp
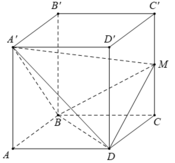
Cho hình hộp chữ nhật ABCD. A'B'C'D' có đáy ABCD là hình vuông cạnh a, AA'=b. Gọi M là trung điểm của cạnh CC'. Tính theo a và b thể tích V của khối tứ diện BDA'M
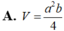
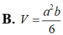
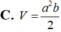
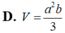
Cho hình lăng trụ ABC.ABC có đáy ABC là tam giác đều cạnh a, tam giác A BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC. Tính cosin góc
α
giữa hai đường thẳng AA và BM.
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, tam giác A' BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC'. Tính cosin góc α giữa hai đường thẳng AA' và BM.
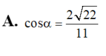
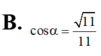
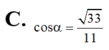
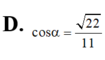
Cho hình hộp ABCD.ABCD có đáy ABCD là hình thoi cạnh a,
B
C
D
^
120
0
,
A
A
7
2
a
. Hình chiếu vuông góc c...
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh a, B C D ^ = 120 0 , A A ' = 7 2 a . Hình chiếu vuông góc của A' lên mạt phẳng (ABCD) trung với giao điểm của AC và BD Tính theo a thể tích khối hộp ABCD.A'B'C'D'?
A. 3 a 3
B. 4 6 a 3 3
C. 2 a 3
D. 3 a 3
Cho hình lăng trụ đứng ABC.ABC có đáy là tam giác vuông BABCa, cạnh bên AAa
2
, M là trung điểm của BC. Khoảng cách giữa AM và B C là:
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông BA=BC=a, cạnh bên AA'=a 2 , M là trung điểm của BC. Khoảng cách giữa AM và B' C là:
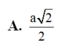
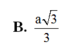
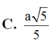
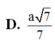
Cho hình lăng trụ ABC.ABC có đáy ABC là tam giác vuông cân tại B và AC2a. Hình chiếu vuông góc của A trên mặt phẳng (ABC) là trung điểm H của cạnh AB và AA
a
2
. Tính thể tích khối lăng trụ ABC.ABC theo a. A.
V
a
3
6
6
B.
V
a
3
3...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B và AC=2a. Hình chiếu vuông góc của A' trên mặt phẳng (ABC) là trung điểm H của cạnh AB và AA' = a 2 . Tính thể tích khối lăng trụ ABC.A'B'C' theo a.
A. V = a 3 6 6
B. V = a 3 3
C. V = a 3 6 2
D. V = a 3 2
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại C, AB 2a, AAa , góc giữa BC và (ABBA) bằng
60
o
. Gọi N là trung điểm AA và M là trung điểm BB. Tính khoảng cách từ điểm M đến mặt phẳng (BCN). A.
2
a
74
37...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại C, AB = 2a, AA'=a , góc giữa BC' và (ABB'A') bằng 60 o . Gọi N là trung điểm AA' và M là trung điểm BB'. Tính khoảng cách từ điểm M đến mặt phẳng (BC'N).
A. 2 a 74 37
B. a 74 37
C. 2 a 37 37
D. a 37 37