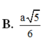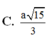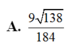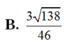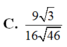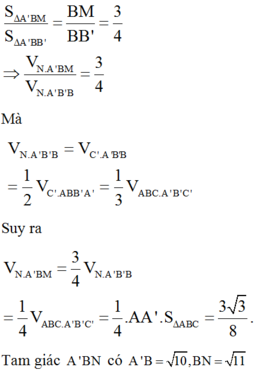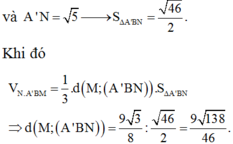Các câu hỏi tương tự
Cho hình lăng trụ đứng ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của CC’. Khoảng cách từ M đến mặt phẳng (A’BC) bằng
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là các tam giác đều cạnh bằng 1,
A
A
3
. Tính khoảng cách d từ điểm A đến mặt phẳng (A’BC)
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là các tam giác đều cạnh bằng 1, A A ' = 3 . Tính khoảng cách d từ điểm A đến mặt phẳng (A’BC)
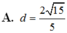
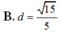
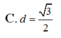
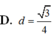
Cho hình lăng trụ ABC.ABC có thể tích bằng V. Gọi M là trung điểm cạnh
B
B
, điểm N thuộc cạnh CC sao cho
C
N
2
C
N
. Tính thể tích khối chóp A.BCNM theo V
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có thể tích bằng V. Gọi M là trung điểm cạnh B B ' , điểm N thuộc cạnh CC' sao cho C N = 2 C ' N . Tính thể tích khối chóp A.BCNM theo V


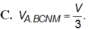

Cho hình lăng trụ tam giác ABC.A’B’C’ có AA’ 1. Xét các điểm M,N,P thay đổi lần lượt trên các cạnh AA’, BB’, CC’ sao cho
A
M
+
B
N
+
C
P
1
. Gọi I là điểm cố định mà mặt phẳng (MNP) luôn đi qua. Độ dài của vecto
u
→
I
A
→
+
I
B...
Đọc tiếp
Cho hình lăng trụ tam giác ABC.A’B’C’ có AA’ = 1. Xét các điểm M,N,P thay đổi lần lượt trên các cạnh AA’, BB’, CC’ sao cho A M + B N + C P = 1 . Gọi I là điểm cố định mà mặt phẳng (MNP) luôn đi qua. Độ dài của vecto u → = I A → + I B → + I C → bằng
![]()
![]()
![]()
![]()
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác cân tại C, AB 2a, AAa , góc giữa BC và (ABBA) bằng
60
o
. Gọi N là trung điểm AA và M là trung điểm BB. Tính khoảng cách từ điểm M đến mặt phẳng (BCN). A.
2
a
74
37...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại C, AB = 2a, AA'=a , góc giữa BC' và (ABB'A') bằng 60 o . Gọi N là trung điểm AA' và M là trung điểm BB'. Tính khoảng cách từ điểm M đến mặt phẳng (BC'N).
A. 2 a 74 37
B. a 74 37
C. 2 a 37 37
D. a 37 37
Cho lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông tại A với AC a
3
. Biết BC’ hợp với mặt phẳng (AA’C’C) với môt góc 300 và hợp với mặt phẳng đáy góc a sao cho
sin
a
6
4
. Gọi M, N lần lượt là trung điểm cạnh BB’ và A’C’. Khoảng cách MN và AC’ là: A. ...
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A với AC= a 3 . Biết BC’ hợp với mặt phẳng (AA’C’C) với môt góc 300 và hợp với mặt phẳng đáy góc a sao cho sin a = 6 4 . Gọi M, N lần lượt là trung điểm cạnh BB’ và A’C’. Khoảng cách MN và AC’ là:
A. a 6 2
B. a 3 6
C. a 5 4
D. a 3
Cho khối lăng trụ ABC.ABC, hình chiếu của điểm A lên mặt phẳng (ABC) là trung điểm M của cạnh BC và AMa
3
, hình chiếu của điểm A lên mặt phẳng (BCCB) là H sao cho MH song song với BB và AHa, khoảng cách giữa hai đường thẳng BB , CC bằng 2a . Thể tích khối lăng trụ đã cho là A.
3
2
a
3
B.
2...
Đọc tiếp
Cho khối lăng trụ ABC.A'B'C', hình chiếu của điểm A lên mặt phẳng (A'B'C') là trung điểm M của cạnh B'C' và A'M=a 3 , hình chiếu của điểm A lên mặt phẳng (BCC'B') là H sao cho MH song song với BB' và AH=a, khoảng cách giữa hai đường thẳng BB' , CC' bằng 2a . Thể tích khối lăng trụ đã cho là
A. 3 2 a 3
B. 2 a 3
C. 2 2 a 3 3
D. 3 2 a 3 2
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với ABACa và cạnh
B
A
C
⏜
120
0
, cạnh bên BBa, gọi I là trung điểm của CC’. Côsin góc tạo bởi mặt phẳng (ABC) và (AB’I) bằng: A.
20
10
B.
3
C. ...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với AB=AC=a và cạnh B A C ⏜ = 120 0 , cạnh bên BB'=a, gọi I là trung điểm của CC’. Côsin góc tạo bởi mặt phẳng (ABC) và (AB’I) bằng:
A. 20 10
B. 3
C. 30 10
D. 30 10
Cho hình lăng trụ đứng có AB a, AC 2a,
A
A
1
2
a
5
và
B
A
C
^
120
0
. Gọi K, I lần lượt là trung điểm của các cạnh
C
C
1
,
B...
Đọc tiếp
Cho hình lăng trụ đứng có AB = a, AC = 2a, A A 1 = 2 a 5 và B A C ^ = 120 0 . Gọi K, I lần lượt là trung điểm của các cạnh C C 1 , B B 1 . Khoảng cách từ điểm I đến mặt phẳng A 1 B K bằng
![]()