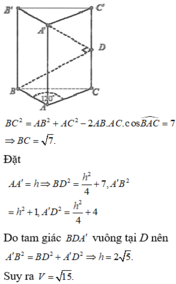Các câu hỏi tương tự
Cho hình lăng trụ đứng ABC.A’B’C’ có AB1, AC2,
B
A
C
^
120
°
. Giả sử D là trung điểm của cạnh CC’ và
B
D
A
^
90
°
. Tính thể tích V của khối lăng trụ ABC.A’B’C’ A.
V
15
2
B. ...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có AB=1, AC=2, B A C ^ = 120 ° . Giả sử D là trung điểm của cạnh CC’ và B D A ^ = 90 ° . Tính thể tích V của khối lăng trụ ABC.A’B’C’
A. V = 15 2
B. V = 3 15
C. V = 3 15 7
D. V = 2 15
Cho lăng trụ tam giác
A
B
C
.
A
B
C
. Mặt phẳng đi qua A, B và trung điểm M của cạnh
C
C
chia lăng trụ thành 2 phần có thể tích
V
1
,
V
2
V
1...
Đọc tiếp
Cho lăng trụ tam giác A B C . A ' B ' C ' . Mặt phẳng đi qua A, B và trung điểm M của cạnh C C ' chia lăng trụ thành 2 phần có thể tích V 1 , V 2 V 1 > V 2 . Tỉ số V 1 V 2 là
A. 4
B. 2
C. 5
D. 3
Cho lăng trụ đứng tam giác
A
B
C
.
A
B
C
.
Gọi M, N, P, Q là các điểm thuộc các cạnh
A
A
,
B
B
,
C
C
,
B
C
thỏa mãn
A
M
A
A...
Đọc tiếp
Cho lăng trụ đứng tam giác A B C . A ' B ' C ' . Gọi M, N, P, Q là các điểm thuộc các cạnh A A ' , B B ' , C C ' , B ' C ' thỏa mãn A M A A ' = 1 2 , B N B B ' = 1 3 , C P C C ' = 1 4 , C ' Q C ' B ' = 1 5 . Gọi V 1 , V 2 lần lượt là thể tích khối tứ diện MNPQ và khối lăng trụ A B C . A ' B ' C ' . Tính tỷ số V 1 V 2 .
A. V 1 V 2 = 11 30
B. V 1 V 2 = 11 45
C. V 1 V 2 = 19 45
D. V 1 V 2 = 22 45
Cho hình lăng trụ đứng ABC.ABC có tất cả các cạnh bằng a . Tính thể tích V của khối lăng trụ ABC.ABC. A.
V
a
3
3
18
B.
V
a
3
2
3
C.
V
a...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có tất cả các cạnh bằng a . Tính thể tích V của khối lăng trụ ABC.A'B'C'.
A. V = a 3 3 18
B. V = a 3 2 3
C. V = a 3 3 9
D. V = a 3 3 6
Cho hình lăng trụ đứng
A
B
C
.
A
B
C
có đáy là tam giác vuông cân tại đỉnh A, mặt bên
B
C
C
B
là hình vuông, khoảng cách giữa
A
B
v
à
C
C
bằng a. Thể tích của khối trụ
A
B
C
.
A
B...
Đọc tiếp
Cho hình lăng trụ đứng A B C . A ' B ' C ' có đáy là tam giác vuông cân tại đỉnh A, mặt bên B C C ' B ' là hình vuông, khoảng cách giữa A B ' v à C C ' bằng a. Thể tích của khối trụ A B C . A ' B ' C ' .
A. a 3
B. 2 a 3 2
C. 2 a 3 3
D. 2 a 3
Cho lăng trụ đứng ABC.ABC có tất cả các cạnh bằng a. Thể tích khối lăng trụ ABC.ABC là A.
3
12
a
3
B.
a
3
C.
3
4
a
3
D.
2
a
3
Đọc tiếp
Cho lăng trụ đứng ABC.A'B'C' có tất cả các cạnh bằng a. Thể tích khối lăng trụ ABC.A'B'C' là
A. 3 12 a 3
B. a 3
C. 3 4 a 3
D. 2 a 3
Cho hình lăng trụ đứng ABC.ABC có AA2a, tam giác ABC vuông tại B có ABa; BC2a. Thể tích khối lăng trụ ABC.ABC là A.
2
a
3
B.
2
a
3
3
C.
4
a
3
3
D.
4...
Đọc tiếp
Cho hình lăng trụ đứng ABC.A'B'C' có AA'=2a, tam giác ABC vuông tại B có AB=a; BC=2a. Thể tích khối lăng trụ ABC.A'B'C' là
A. 2 a 3
B. 2 a 3 3
C. 4 a 3 3
D. 4 a 3
Cho hình lăng trụ
A
B
C
.
A
B
C
có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C lên mặt phẳng
A
B
B
A
là tâm của hình bình hành
A
B
B
A
. Thể tích khối lăng trụ
A
B...
Đọc tiếp
Cho hình lăng trụ A B C . A ' B ' C ' có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C lên mặt phẳng A B B ' A ' là tâm của hình bình hành A B B ' A ' . Thể tích khối lăng trụ A B C . A ' B ' C ' tính theo a là:
A. a 3 2 4
B. a 3 2 12
C. a 3 3
D. a 3 3 4
Cho hình lăng trụ ABC.ABC có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C lên mặt phẳng (ABBA) là tâm của hình bình hành ABBA. Thể tích khối lăng trụ ABC.ABC tính theo a là: A.
a
3
2
4
B.
a
3
2...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có độ dài tất cả các cạnh bằng a và hình chiếu vuông góc của đỉnh C lên mặt phẳng (ABB'A') là tâm của hình bình hành ABB'A'. Thể tích khối lăng trụ ABC.A'B'C' tính theo a là:
A. a 3 2 4
B. a 3 2 12
C. a 3 3
D. a 3 3 4