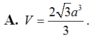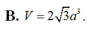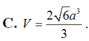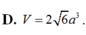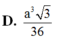Trên tia đối của ia B'A', lấy D sao cho B'A'=B'D
Ta có: B'A'=B'D
B'A'=BA
Do đó: B'D=BA
Ta có: B'A'//BA
=>B'D//AB
Xét tứ giác AB'DB có
AB//B'D
AB=B'D
Do đó: AB'DB là hình bình hành
=>AB'//BD
mà AB'⊥BC'
nên BD⊥BC'
Đặt BB'=AA'=CC'=h
Vì ABC.A'B'C' là lăng trụ đứng nên BB'⊥(A'B'C')
=>BB'⊥B'C'
=>ΔBB'C' vuông tại B'
=>\(\left(BB^{\prime}\right)^2+\left(B^{\prime}C^{\prime}\right)^2=C^{\prime}B^2\)
=>\(C^{\prime}B^2=h^2+a^2\)
Xét ΔC'A'D có
CB' là đường trung tuyến
\(CB^{\prime}=\frac{A^{\prime}D}{2}\left(=a\right)\)
Do đó: ΔC'A'D vuông tại C'
=>\(\left(C^{\prime}A^{\prime}\right)^2+\left(C^{\prime}D\right)^2=\left(A^{\prime}D\right)^2\)
=>\(\left(C^{\prime}D\right)^2=\left(A^{\prime}D\right)^2-\left(A^{\prime}C^{\prime}\right)^2=\left(2a\right)^2-a^2=3a^2\)
ΔBB'D vuông tại B'
=>\(BD^2=\left(BB^{\prime}\right)^2+\left(B^{\prime}D\right)^2=h^2+a^2\)
ΔBDC' vuông tại B
=>\(BD^2+\left(BC^{\prime}\right)^2=\left(DC^{\prime}\right)^2\)
=>\(h^2+a^2+h^2+a^2=3a^2\)
=>\(a^2=2h^2\)
=>\(h^2=\frac{a^2}{2}\)
=>\(h=\frac{a\sqrt2}{2}\)
ΔABC đều nên \(S_{đáy}=AB^2\cdot\frac{\sqrt3}{4}=\frac{a^2\sqrt3}{4}\)
Thể tích hình chóp là: \(V=\frac13\cdot\frac{a\sqrt2}{2}\cdot\frac{a^2\sqrt3}{4}=\frac{a^3\sqrt6}{24}\)