Đáp án A
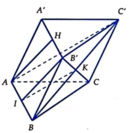
Gọi ![]() và I là trung điểm của AB
và I là trung điểm của AB
Do HB' = AI, HB'//AI => AHB'I là hình bình hành => AH//B'I
Mặt khác KI//AC' nên (AHC')//(B'CI)=> B'C//(AHC')
Đáp án A

Gọi ![]() và I là trung điểm của AB
và I là trung điểm của AB
Do HB' = AI, HB'//AI => AHB'I là hình bình hành => AH//B'I
Mặt khác KI//AC' nên (AHC')//(B'CI)=> B'C//(AHC')
Cho hình lăng trụ ABCD.A’B’C’D”. Gọi H là trung điểm của A’B’. Đường thẳng B’C song song với mặt phẳng nào sau đây?
A. ( AHC’)
B. (AA’H)
C. ( HAB)
D. ( HA’C’)
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB = a, AC = a 3 Hình chiếu vuông góc của A' lên mặt phẳng (ABC) là trung điểm H của BC, HA' = a 5 Gọi φ là góc giữa hai đường thẳng A'B và B'C.
Tính cos φ
A.cos φ = 7 3 48
B. cos φ = 3 2
C. cos φ = 1 2
D. cos φ = 7 3 24
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi H là trung điểm của A'B'.
a) Chứng minh rằng CB′ // (AHC′)
b) Tìm giao tuyến d của (AB'C') và (ABC)
Cho hình lăng trụ đều ABC.A'B'C' có góc giữa đường thẳng A'B với mặt phẳng (ABC) bằng 60 0 và khoảng cách từ điểm A đến mặt phẳng (A'BC) bằng a 5 2 . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'.
A . V = 125 3 96 a 3
B . V = 125 3 288 a 3
C . V = 125 3 384 a 3
D . V = 125 3 48 a 3
Cho lăng trụ ABC.A'B'C' Gọi M,N lần lượt là trung điểm của A'B' và CC' . Khi đó CB' song song với
A. AM
B. (BC'M)
C. A'N
D. (AC'M)
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’.
a) Chứng minh rằng AM song song với A’M’.
b) Tìm giao điểm của mặt phẳng (A’B’C’) với đường thẳng A’M.
c) Tìm giao tuyến d của hai mặt phẳng (AB’C’) và (BA’C’).
d) Tìm giao điểm G của đường thẳng d với mp(AMA’). Chứng minh G là trọng tâm của tam giác AB’C’.
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông cân tại B, AC = 2a, hình chiếu vuông góc của A' lên ABC là trung điểm H của AC. Đường thẳng A'B tạo với (ABC) một góc 45 0 . Phát biểu nào sua đây là đúng?
A . A ' B ⊥ B C
B. Thể tích khối (ABC.A'B'C') là a 3 3
C . A H = a 2 2
D . A ' B A ^ = 45 0
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác ABC đều cạnh a . Gọi I là trung điểm AB , hình chiếu của điểm A' lên (ABC ) là trung điểm H của đoạn CI , góc giữa đường thẳng AA' và mặt phẳng (ABC ) bằng 45 độ. Tính khoảng cách giữa hai đường thẳng chéo nhau A A' và CI
Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi H là trực tâm của tam giác ABC và biết rằng A'H vuông góc với mặt phẳng (ABC). Chứng minh rằng:
a) AA ⊥ BC và AA' ⊥ B'C'.
b) Gọi MM' là giao tuyến của mặt phẳng (AHA') với mặt bên BCC'B', trong đó M ∈ BC và M' ∈ B'C'. Chứng minh rằng tứ giác BCC'B là hình chữ nhật và MM' là đường cao của hình chữ nhật đó.