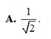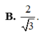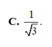Các câu hỏi tương tự
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB a, BC
a
2
, AA
a
3
. Gọi a là góc giữa 2 mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ). Giá trị tana bằng: A. 2
Đọc tiếp
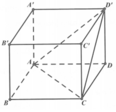
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = a 2 , AA' = a 3 .
Gọi a là góc giữa 2 mặt phẳng (ACD’) và (ABCD) (tham khảo hình vẽ).
Giá trị tana bằng:
A. 2
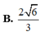
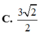
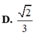
Cho hình hộp chữ nhật ABCD.ABCD có đáy là hình chữ nhật , AB a, AD 2, hình chiếu vuông góc của điểm A trên mặt phẳng
(
A
B
C
D
)
là trung điểm H của A’D’. Biết rằng AA’ hợp với đáy một góc
60
0
. Gọi
α
là số đo của góc giữa hai đường thẳng
A
C
,
B...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có đáy là hình chữ nhật , AB = a, AD = 2, hình chiếu vuông góc của điểm A trên mặt phẳng ( A ' B ' C ' D ' ) là trung điểm H của A’D’. Biết rằng AA’ hợp với đáy một góc 60 0 . Gọi α là số đo của góc giữa hai đường thẳng A C , B ' D . Khi đó cos α bằng
![]()
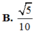
![]()
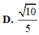
Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với AB
6
, AD
3
, AC3 và mặt phẳng (AACC) vuông góc với mặt đáy. Biết hai mặt phẳng (AACC); (AABB) tạo với nhau góc
α
thỏa mãn tan
α
3
4
. Thể tích khối lăng trụ ABCD.A’B’C’D’ bằng A. V8 B. V12 C. V10 D. V6
Đọc tiếp
Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với AB= 6 , AD= 3 , A'C=3 và mặt phẳng (AA'CC') vuông góc với mặt đáy. Biết hai mặt phẳng (AA'CC'); (AA'BB') tạo với nhau góc α thỏa mãn tan α = 3 4 . Thể tích khối lăng trụ ABCD.A’B’C’D’ bằng
A. V=8
B. V=12
C. V=10
D. V=6
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a
3
, BD3a. Hình chiếu vuông góc của B trên mặt phẳng (ABCD) trùng với trung điểm A’C’. Gọi
α
là góc giữa 2 mặt phẳng (ABCD) và (CDDC). Thể tích của khối hộp ABCD.ABCD bằng
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a 3 , BD=3a. Hình chiếu vuông góc của B trên mặt phẳng (A'B'C'D') trùng với trung điểm A’C’. Gọi α là góc giữa 2 mặt phẳng (ABCD) và (CDD'C'). Thể tích của khối hộp ABCD.A'B'C'D' bằng
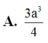
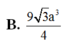
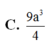
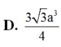
Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với
A
B
6
,
A
D
3
,
A
C
3
và mặt phẳng (AACC) vuông góc với mặt đáy. Biết hai mặt phẳng (AACC), (AABB) tạo với nhau góc
α
thỏa mãn
tan
α
3
4
. Thể tích khối lăng trụ AB...
Đọc tiếp
Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với A B = 6 , A D = 3 , A ' C = 3 và mặt phẳng (AA'C'C) vuông góc với mặt đáy. Biết hai mặt phẳng (AA'C'C), (AA'B'B) tạo với nhau góc α thỏa mãn tan α = 3 4 . Thể tích khối lăng trụ ABCD.A’B’C’D’ bằng
A. V=8
B. V=12
C. V=10
D. V=6
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = 2a, AA’ = a. Lấy điểm M trên cạnh AD sao cho AM = 3MD. Tính khoảng cách từ M đến mặt phẳng (AB’C).
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a,
BCD
^
120° và AA 7a/2. Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’. A. V 12
a
3
B. V 3
a
3
C. V 9
a
3
D. V 6
a
3
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a, BCD ^ = 120° và AA' = 7a/2. Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.

A. V = 12 a 3
B. V = 3 a 3
C. V = 9 a 3
D. V = 6 a 3
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi tâm O, cạnh bằng a, BDa
3
. Góc giữa CC’ và mặt đáy là
60
0
, trung điểm H của AO là hình chiếu vuông góc của A’ lên mặt phẳng ABCD. Tính thể tích của hình hộp
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi tâm O, cạnh bằng a, B'D'=a 3 . Góc giữa CC’ và mặt đáy là 60 0 , trung điểm H của AO là hình chiếu vuông góc của A’ lên mặt phẳng ABCD. Tính thể tích của hình hộp
![]()
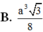
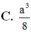
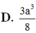
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, SH HC, SA AB. Gọi
α
là góc giữa đường thẳng SC và mặt phẳng (ABCD). Tính giá trị của
tan
α
.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt phẳng (SAB) vuông góc với đáy (ABCD). Gọi H là trung điểm của AB, SH = HC, SA = AB. Gọi α là góc giữa đường thẳng SC và mặt phẳng (ABCD). Tính giá trị của tan α .