Chọn D
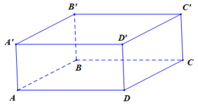
Ta có 2 mặt phẳng ( ABCD) và ( A’B’C’D’) là 2 mặt phẳng song song nên
d((ABCD), (A’B’C’D’))=AA’ ( AA’ là đoạn vuông góc chung của 2 mặt phẳng)

Chọn D
Ta có 2 mặt phẳng ( ABCD) và ( A’B’C’D’) là 2 mặt phẳng song song nên
d((ABCD), (A’B’C’D’))=AA’ ( AA’ là đoạn vuông góc chung của 2 mặt phẳng)
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có AB =a, AD = 2a, AA’ =a. Gọi M là điểm trên đoạn AD với A D M D . Gọi x là độ dài khoảng cách giữa hai đường thẳng AD', B 'C và y là độ dài khoảng cách từ M đến mặt phẳng (AB’C). Tính giá trị xy
A. 5 a 5 3
B. a 2 2
C. 3 a 2 4
D. 3 a 2 2
Cho hình hộp thoi ABCD.A’B’C’D’ có các cạnh đều bằng a và B A D ^ = B A A ' ^ = D A A ' ^ = 60 ° . Tính khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’).
A. a 5 5
B. a 6 3
C. a 10 5
D. a 3 3
Cho lăng trụ ABCD. A’B’C’D’ có đáy ABCD là hình chữ nhật với AB =a, AD = a 3 Hình chiếu vuông góc của A' lên (ABCD) trùng với giao điểm của AC và BD. Tính khoảng cách từ điểm B' đến mặt phẳng (A’BD)
A. a 3
B. a 2
C. a 3 2
D. a 3 6
Cho hình hộp chữ nhật ABCD. A’B’C’D’ có diện tích các mặt ABCD, BCC’B’, CDD’C’ lần lượt là 2 a 2 , 3 a 2 , 6 a 2 . Tính thể tích khối hộp chữ nhật ABCD. A’B’C’D’
A. 36 a 3
B. 6 a 3
C. 36 a 6
D. 6 a 2
Cho hình lập phương ABCD. A’B’C’D’ cạnh a. Gọi N là trung điểm của cạnh CC’. Mặt phẳng (NAB) cắt hình hộp theo thiết diện là hình chữ nhật có chu vi là:
![]()
![]()
![]()
D. Cả A, B, C đều sai
Cho hình lập phương ABCD. A’B’C’D’ cạnh a. Tính khoảng cách từ điểm A đến mặt phẳng (A’BC) theo a
A. a 2 2
B. a 3 3
C. a 3 2
D. a 2 3
Cho hình lập phương ABCD. A’B’C’D’ cạnh bằng a. Gọi K là trung điểm DD'. Tính khoảng cách giữa hai đường thẳng CK và A’D.
A. 4 a 3
B. a 3
C. 2 a 3
D. 3 a 4
Cho hình lập phương ABCD. A’B’C’D’. AA’ vuông góc với mặt phẳng.
A. (CDD’C’)
B. (BCD)
C. (BCC’B’)
D. (A’BD)
Cho hình hộp ABCD. A’B’C’D’ gọi O là giao điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’ điểm của AC và BD. Tính tỉ số thể tích của khối chóp O. ABC và khối hộp ABCD. A’B’C’D’
A. 1 4
B. 1 3
C. 1 6
D. 1 12