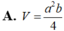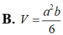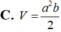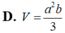Đáp án D
V I . B C D = 1 3 d ( I , ( B C D ) ) S B C D = 2 a 3
Đáp án D
V I . B C D = 1 3 d ( I , ( B C D ) ) S B C D = 2 a 3
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’
Cho hình hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, hình chiếu của A' lên đáy (ABCD) trùng với trung điểm của cạnh AD. Biết rằng AB = a, AD = 2a và thể tích hình hộp đã cho bằng 2 a 3 . Khoảng cách từ B đến mặt phẳng (A'DCB') bằng:
A. 2 a 6 B. 2 a 3
C. 3 a 3 D. a 2
Cho hình chóp tứ giác S.ABCD có thể tích bằng V. Lấy điểm A' trên cạnh SA sao cho SA' = SA/3. Mặt phẳng qua A' và song song với đáy của hình chóp cắt cạnh SB, SC, SD lần lượt tại B', C', D'. Thể tích hình chóp S.A'B'C'D' bằng:
A. V/3 B. V/9
C. V/27 D. V/81.
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = 2a, AD = 3a, AA’ = a 2 . Gọi I là trung điểm của cạnh B’C’. Thể tích khối chóp I.BCD bằng.
A. 3 a 3
B. a 3
C. 3 a 3
D. 2 a 3
Cho hình chóp tam giác S.ABC có SA vuông góc với mặt đáy, tam giác ABC cân tại A. Trên cạnh AB lấy điểm D sao cho AB = 3AD. Gọi H là hình chiếu của B lên CD, M là trung điểm CH. Tính theo a thể tích khối chóp S.ABM biết SA = AM = a và BM = 2/3 a
Cho hình lăng trụ ngũ giác ABCD.A'B'C'D'. Gọi A'', B'', C'', D'', E'' lần lượt là trung điểm của các cạnh AA', BB', CC', DD', EE'. Tỉ số thể tích giữa khối lăng trụ ABCDE.A''B''C''D''E'' và khối lăng trụ ABCDE.A'B'C'D' bằng:
A. 1/2 B. 1/4
C. 1/8 D. 1/10.
Câu 1: Cho hình chóp tứ giác đều S.ABCD có đáy bằng a, và cạnh bên bằng a√2.
a) Tính thể tích của hình chóp đã cho.
b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
c) Gọi A’ và C' lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hình chóp A’.ABCD và C’.CBAD bằng nhau.
Câu 2: Trong không gian tọa độ Oxyz cho các điểm A(4; -1; 2); B(1; 2; 2), C(1; -1; 5)
a) Chứng minh rằng ABC là tam giác đều.
b) Viết Phương trình mp(ABC). Tính thể tích khối tứ diện giới hạn bởi mp(ABC) và các mặt phẳng tọa độ.
c) Viết phương trình trục của đường tròn ngoại tiếp ΔABC
d) Tìm tọa độ điểm D sao cho ABCD là tứ diện đều.
các bạn giúp mình với
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
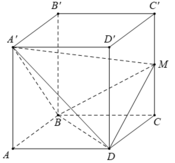
Cho hình hộp chữ nhật ABCD. A'B'C'D' có đáy ABCD là hình vuông cạnh a, AA'=b. Gọi M là trung điểm của cạnh CC'. Tính theo a và b thể tích V của khối tứ diện BDA'M