Phép đối xứng qua mặt phẳng (BDD’B’) biến lăng trụ ABD.A’B’D’ thành BCD.B’C’D’
⇒ hai lăng trụ ABD.A’B’D’ và BCD.B’C’D’ bằng nhau.
Phép đối xứng qua mặt phẳng (BDD’B’) biến lăng trụ ABD.A’B’D’ thành BCD.B’C’D’
⇒ hai lăng trụ ABD.A’B’D’ và BCD.B’C’D’ bằng nhau.
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng hai tứ diện A’ABD và CC’D’B’ bằng nhau.
Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với A B = 6 , A D = 3 , A ' C = 3 và mặt phẳng (AA'C'C) vuông góc với mặt đáy. Biết hai mặt phẳng (AA'C'C), (AA'B'B) tạo với nhau góc α thỏa mãn tan α = 3 4 . Thể tích khối lăng trụ ABCD.A’B’C’D’ bằng
A. V=8
B. V=12
C. V=10
D. V=6
Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật với AB= 6 , AD= 3 , A'C=3 và mặt phẳng (AA'CC') vuông góc với mặt đáy. Biết hai mặt phẳng (AA'CC'); (AA'BB') tạo với nhau góc α thỏa mãn tan α = 3 4 . Thể tích khối lăng trụ ABCD.A’B’C’D’ bằng
A. V=8
B. V=12
C. V=10
D. V=6
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng 2a. Một hình trụ có hai đáy là hai hình tròn nội tiếp trong hai hình vuông ABCD và A’B’C’D’. Tính thể tích của khối lăng trụ tạo nên từ hình trụ trên.
A. 2 π a 3 .
B. π a 3 .
C. 2 2 π a 3 .
D. 4 π a 3 .
Cho lăng trụ lục giác đều ABCDEF.A'B'C'D'E'F'. O và O' là tâm đường tròn ngoại tiếp hai đáy, mặt phẳng (P) đi qua trung điểm của OO' và cắt các cạnh bên của lăng trụ. Chứng minh rằng (P) của lăng trụ đã cho thành hai đa diện có thể tích bằng nhau
Cho lăng trụ ABC.A’B’C’. Gọi E, F, G lần lượt là trung điểm của AA’, BB’, CC’. Chứng minh rằng các lăng trụ ABC.EFG và EFG.A’B’C’ bằng nhau
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi, biết AA’=4a, AC=2a, BD=a. Thể tích của khối lăng trụ là:
A. 2a3
B. 8a3
C. 6a3
D. 4a3.
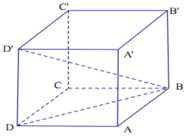
Lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh a và đường chéo BD’ của lăng trụ hợp với đáy ABCD một góc 30º. Thể tích của lăng trụ là:
A. a 3 6 3
B. a 3 6 8
C. a 3 3
D. 3 a 3 6
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là hình thoi, biết AA’ = 4a; AC = 2a, BD = a. Thế tích V của khối lăng trụ là
![]()
![]()
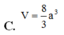
![]()