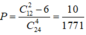Chọn đáp án D
Phương pháp
Nhận xét rằng: Đa giác đều có số đỉnh chẵn luôn tồn tại đường kính của đường tròn ngoại tiếp đa giác là đoạn nối hai đỉnh của đa giác.
Nên ta chia đường tròn ngoại tiếp đa giác đều đó thành hai nửa đường tròn và dựa vào tính đối xứng của các đỉnh để tạo thành một hình chữ nhật.
Tính số hình vuông trong các hình chữ nhật đó để tính xác suất 4 đỉnh tạo thành hình chữ nhật mà không phải hình vuông.
Cách giải
Số phần tử của không gian mẫu n Ω = C 24 4
Ta vẽ đường tròn ngoại tiếp đa giác đều 24 đỉnh. Vẽ một đường kính của đường tròn này. Khi đó hai nửa đường tròn đều chứa 12 đỉnh.
Với mỗi đỉnh thuộc nửa đường tròn thứ nhất ta đều có một đỉnh đối xứng với nó qua đường kính và thuộc nửa đường tròn còn lại.
Như vậy cứ hai đỉnh thuộc nửa đường tròn thứ nhất ta xác định được hai đỉnh đối xứng với nó qua đường kính và thuộc nửa đường tròn còn lại, bốn đỉnh này tạo thành một hình chữ nhật.
Vậy số hình chữ nhật có 4 đỉnh là các đỉnh của đa giác đã cho là C 12 2 .
Nhận thấy rằng trong số các hình chữ nhật tạo thành có 24:4=6 hình vuông (vì hình chữ nhật có các cạnh bằng nhau là hình vuông)
Nên số hình chữ nhật mà không phải hình vuông là C 12 2 - 6 .
Xác suất cần tìm là