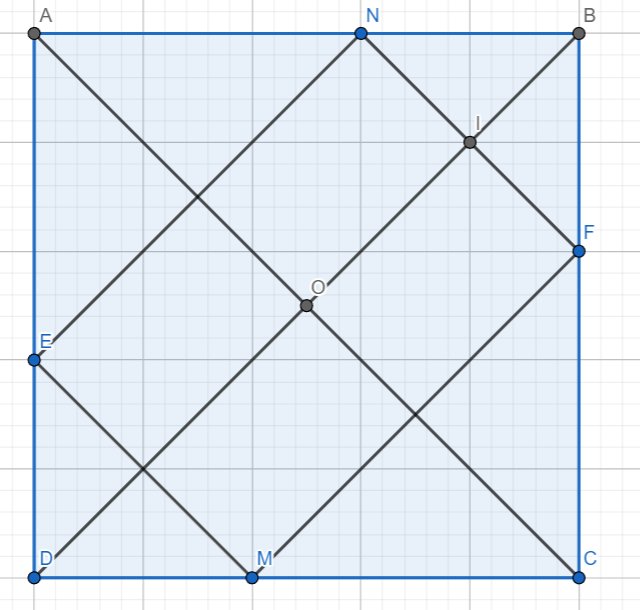
a) Ta có :
\(\widehat{BNF}=\widehat{BAC}\left(đồng.vị\right)\)
\(\widehat{BAC}=\widehat{ACD}\left(so.le.trong\right)\)
\(\widehat{ACD}=\widehat{EMD}\left(đồng.vị\right)\)
\(\Rightarrow\widehat{BNF}=\widehat{EMD}\left(1\right)\)
Xét \(\Delta AON\&\Delta COM:\)
\(\widehat{MOC}=\widehat{NOA}\left(đối.đỉnh\right)\)
\(\widehat{NAO}=\widehat{OCM}\left(so.le.trong\right)\)
\(\Rightarrow\Delta AON\sim\Delta COM\left(g.g\right)\)
\(\Rightarrow\dfrac{AN}{MC}=\dfrac{OA}{OC}=1\) (\(O\) là trung điểm \(AC\) - tính chất HCN)
\(\Rightarrow AN=MC\)
mà \(AB=AN+NB=CD=MC+MD\) (tính chất HCN)
\(\Rightarrow NB=MD\)
Xét \(\Delta EDM\&\Delta FBN:\)
\(\widehat{BNF}=\widehat{EMD}\left(do.\left(1\right)\right)\)
\(\widehat{EDM}=\widehat{FBN}=90^o\left(HCN\right)\)
\(NB=MD\left(cmt\right)\)
\(\Rightarrow\Delta EDM=\Delta FBN\left(g.c.g\right)\)
\(\Rightarrow ME=NF\)
b) Ta có: \(ME//NF\) (cùng song song với \(AC\))
mà \(ME=NF\left(cmt\right)\)
\(\Rightarrow MENF\) là hình bình hành
\(\Rightarrow EN//MF//BD\) (tính chất đối xứng của HCN \(ABCD\) và tính chất của hình bình hành \(MENF\))
mà \(BD\) cắt \(NF\) tại \(I\left(gt\right)\)
\(\Rightarrow OI//MF\)
mà \(O\) là trọng tâm \(MENF\&ABCD\) (tính chất HCN và HBH)
\(\Rightarrow I\) là trung điểm \(NF\left(đpcm\right)\)