Question

Cho hình chữ nhật ABCD. Lấy điểm E thuộc AB sao cho AE=2/3 AB. F là trung điểm của DC. G là giao điểm của AF và DB. H là giao điểm của DB và EC. Tổng của diện tích tam giác GDF và tam giác EHB bằng 7 cm^2. Tính diện tích của hình chữ nhật ABCD và tỉ lệ của BH/GD?

Answer 1

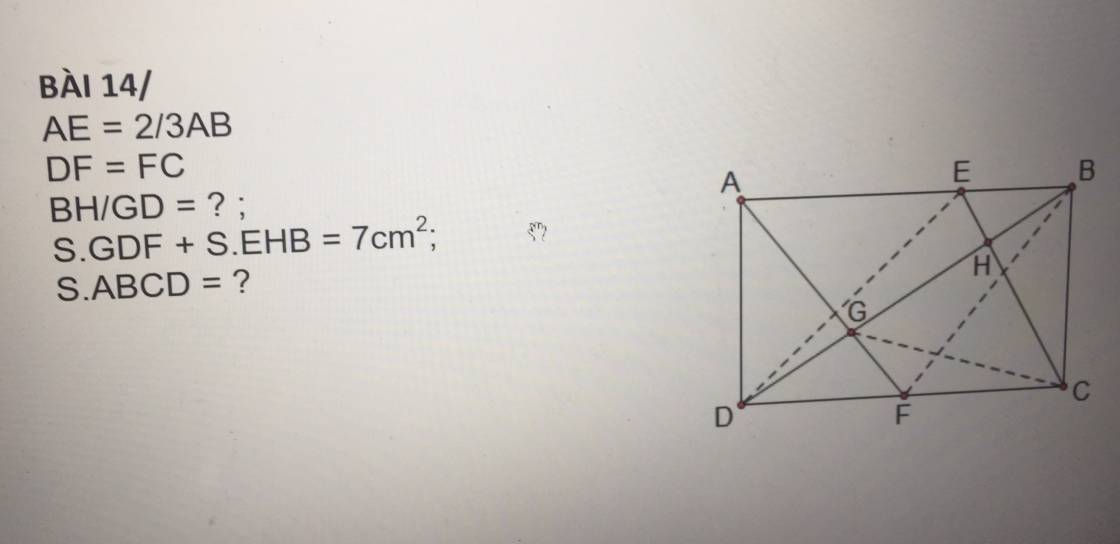
Ta có: AE+EB=AB

=>\(EB=AB-AE=AB-\frac23\times AB=\frac13\times AB\)

mà AB=CD

nên \(EB=\frac13\times CD\)

ΔEBC vuông tại B

=>\(S_{BEC}=\frac12\times BE\times BC=\frac12\times\frac13\times AB\times BC=\frac16\times S_{ABCD}\)

Vì EB//DC

nên \(\frac{HE}{HC}=\frac{EB}{DC}=\frac13\)

=>HC=3xHE

Ta có: HC+HE=EC

=>EC=HE+3xHE=4xHE

=>\(EH=\frac14\times EC\)

=>\(S_{EHB}=\frac14\times S_{EBC}=\frac14\times\frac16\times S_{ABCD}=\frac{1}{24}\times S_{ABCD}\)

DF=FC

=>F là trung điểm của DC

=>\(DF=FC=\frac12\times DC\)

ΔADF vuông tại D

=>\(S_{ADF}=\frac12\times DA\times DF=\frac12\times DA\times\frac12\times DC=\frac14\times S_{ABCD}\)

Vì AB//CD

nên \(\frac{GA}{GF}=\frac{AB}{DF}=2\)

=>GA=2GF

Ta có: GA+GF=AF

=>AF=2GF+GF=3GF

=>\(S_{ADF}=3\times S_{GDF}\)

=>\(S_{GDF}=\frac13\times S_{ADF}=\frac13\times\frac14\times S_{ABCD}=\frac{1}{12}\times S_{ABCD}\)

Ta có: \(S_{GDF}+S_{HEB}=7\)

=>\(\frac{1}{24}\times S_{ABCD}+\frac{1}{12}\times S_{ABCD}=7\)

=>\(\frac{3}{24}\times S_{ABCD}=7\)

=>\(\frac{S_{ABCD}}{8}=7\)

=>\(S_{ABCD}=8\times7=56\left(\operatorname{cm}^2\right)\)