Chọn B.
Xét đáp án B
Đặt ![]() và BA = a; BC = b và BK = c.
và BA = a; BC = b và BK = c.
Do M là trung điểm của AK nên ![]() ,
,
![]()
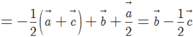
Do đó 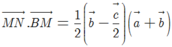


Vì ![]() và
và ![]() nên
nên ![]()
Suy ra MN và BM vuông góc với nhau
Do đó góc BMN bằng 900.
Chọn B.
Xét đáp án B
Đặt ![]() và BA = a; BC = b và BK = c.
và BA = a; BC = b và BK = c.
Do M là trung điểm của AK nên ![]() ,
,
![]()
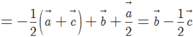
Do đó 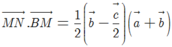


Vì ![]() và
và ![]() nên
nên ![]()
Suy ra MN và BM vuông góc với nhau
Do đó góc BMN bằng 900.
Cho hình chữ nhật ABCD. Kẻ BK vuông góc với AC. Gọi M , N lần lượt là trung điểm AK và CĐ . Biết B(1;2), N(-3;0) . Viết phương trình đường tròn ngoại tiếp tam giác BM
Cho hình chữ nhật ABCD. Kẻ BK⊥AC. Gọi M,N lần lượt là trung điểm của AK và CD
Chứng minh: (BMN) ̂=90^0. Tìm điều kiện của hình chữ nhật để tam giác BMN vuông cân.
Trong các mệnh đề sau
a. Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
b. Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó.
c. Góc tạo bởi hai tia phân giác của hai góc kề bù là góc nhọn.
d. Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến dường thẳng đó, đường vuông góc là đường dài nhất.
Số mệnh đề đúng là:
A. 1.
B. 2
C. 3
D. 4
Cho hình chữ nhật ABCD ; AH vuông góc với BD tại H . Gọi I ; M lần lượt là trung điểm của BH và CD .
IK vuông góc với AM tại K . CMR :
IA2 + IM2 = BC2 + 1/4 CD2
cho HCN ABCD , H là hình chiếu của B lên AC .M là trung điểm của AH và N là trung điểm của BH qua M kẻ đg thẳng vuông góc với BM cắt CD tại K . CMR MKCN là hbh
Cho tam giác ABC nhọn(AB<AC) nội tiếp đường tròn nội tiếp đường tròn
tâm O
ĐỀ SỐ 2
Kẻ đường cao AH. Gọi M, N là hình chiếu vuông góc của H lên AB, AC. Kẻ NE
vuông góc với AH. Đường thẳng vuông góc với AC kẻ từ C cắt đường tròn tại I và
cắt tia AH tại D. Tia AH cắt đường tròn tại F
a) Chứng minh ABC+ACB=AIC và tứ giác DENC nội tiếp.
b) Chứng minh AM. AB = AN . AC.
c) Chứng minh tứ giác BFIC là hình thang cân.
d) Chứng minh tứ giác BMED nội tiếp .
Cho tam giác ABC có AB=6cm, AC=8cm và góc A=600 .Gọi M là trung điểm của BC. Qua B kẻ một đường thẳng vuông góc với AM cắt AC tại N. Tính tỉ số \(\dfrac{AN}{AC}\)
Cho tam giác ABC vuông tại A, góc B = 60. Gọi I là trung điểm cạnh BC.Trên các cạnh AB,AC lần lượt lấy các điểm M,N.Chứng minh rằng MI vuông góc với NI khi và chỉ khi BM + căn 3 CN = BC
Cho tứ giác ABCD. Cho hai đường chéo AC và BD vuông góc với nhau. Tìm mệnh đề đúng?
A. AB2 + BC2 = CD2 + AD2
B. AB2 = BC2 + CD2
C. BC2 = AD2 + CD2
D. AB2 + CD2 = BC2 + AD2