24 tháng 11 2021 lúc 13:54
Các câu hỏi tương tự
Cho hình vuông ABCD,gọi E,F lần lượt là trung điểm của BC,CD ; H là giao của AE,BF. K là hình chiếu của D lên AH. CMR
a) AE vuông góc BF
b) Tính \(\dfrac{AH}{AE},\dfrac{BH}{BF}\)
c) K là trung điểm AH
26 tháng 5 2022 lúc 20:23
Trong mặt phẳng tọa độ oxy cho hình thang ABCD vuông tại A và D có CD = 2AB và B ( 2;3 ), gọi E là trung điểm của cạnh CD, H là hình chiếu vuông góc của E lên AC, biết phương trình đường thẳng DH: x + 2y -3 = 0 và đường thẳng AC di qua k ( 1;3 )
Cho hình chữ nhật ABCD ; AH vuông góc với BD tại H . Gọi I ; M lần lượt là trung điểm của BH và CD .
IK vuông góc với AM tại K . CMR :
IA2 + IM2 = BC2 + 1/4 CD2
Cho tam giác ABC cân tại A, M trung điểm BC, H là hình chiếu của M trên AC , E là trung điểm MH . Chứng minh AE vuông góc với BH
Cho tam giác ABC có AB=6cm, AC=8cm và góc A=600 .Gọi M là trung điểm của BC. Qua B kẻ một đường thẳng vuông góc với AM cắt AC tại N. Tính tỉ số \(\dfrac{AN}{AC}\)
Cho hình bình hành ABCD có tâm I, đường thẳng qua B vuông góc với BD cắt AI tại M, đường thẳng qua D vuông góc với BD cắt AB tại N. Biết pt DM: x+y-4=0, điểm E(5;0) thuộc NI, trung điểm của BI là P(-1/2;-3). Tìm tọa độ A,B,C,D
Cho tam giác ABC nhọn(AB<AC) nội tiếp đường tròn nội tiếp đường tròntâm OĐỀ SỐ 2Kẻ đường cao AH. Gọi M, N là hình chiếu vuông góc của H lên AB, AC. Kẻ NEvuông góc với AH. Đường thẳng vuông góc với AC kẻ từ C cắt đường tròn tại I vàcắt tia AH tại D. Tia AH cắt đường tròn tại Fa) Chứng minh ABC+ACBAIC và tứ giác DENC nội tiếp.b) Chứng minh AM. AB AN . AC.c) Chứng minh tứ giác BFIC là hình thang cân.d) Chứng minh tứ giác BMED nội tiếp .
Đọc tiếp
Cho tam giác ABC nhọn(AB<AC) nội tiếp đường tròn nội tiếp đường tròn
tâm O
ĐỀ SỐ 2
Kẻ đường cao AH. Gọi M, N là hình chiếu vuông góc của H lên AB, AC. Kẻ NE
vuông góc với AH. Đường thẳng vuông góc với AC kẻ từ C cắt đường tròn tại I và
cắt tia AH tại D. Tia AH cắt đường tròn tại F
a) Chứng minh ABC+ACB=AIC và tứ giác DENC nội tiếp.
b) Chứng minh AM. AB = AN . AC.
c) Chứng minh tứ giác BFIC là hình thang cân.
d) Chứng minh tứ giác BMED nội tiếp .
Câu 4. Bạn hãy giúp bạn Toàn làm công việc sau: Cho đoạn thẳng BC cố định có độ dài bằng 4, gọi M, N lần lượt là trung điểm của các đoạn thẳng BC, BM. Trên đường thẳng vuông góc BC tại N lấy điểm A bất kì, gọi H là trực tâm của tam giác ABC, BH cắt AC tại K. Em hãy giúp Toàn tìm giá trị lớn nhất của diện tích tam giác BMK?
Đọc tiếp
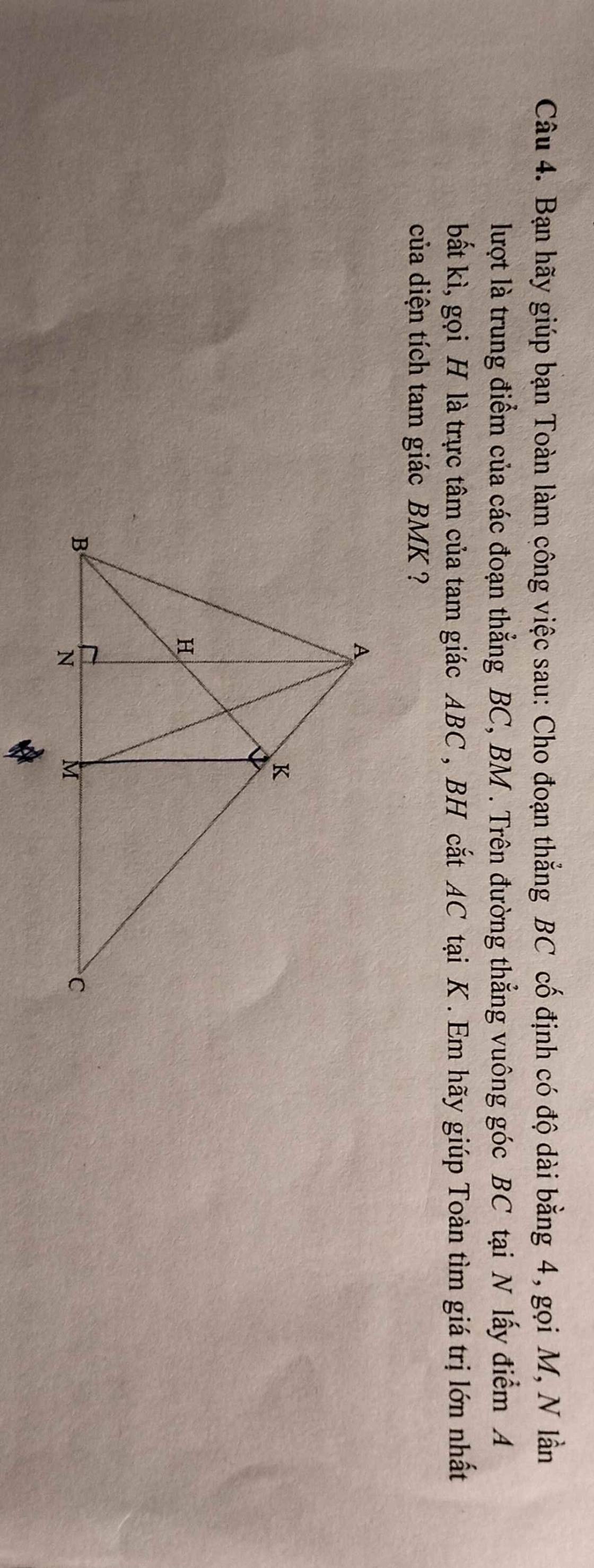Câu 4. Bạn hãy giúp bạn Toàn làm công việc sau: Cho đoạn thẳng BC cố định có độ dài bằng 4, gọi M, N lần lượt là trung điểm của các đoạn thẳng BC, BM. Trên đường thẳng vuông góc BC tại N lấy điểm A bất kì, gọi H là trực tâm của tam giác ABC, BH cắt AC tại K. Em hãy giúp Toàn tìm giá trị lớn nhất của diện tích tam giác BMK?
Cho hình chữ nhật ABCD. Kẻ BK vuông góc với AC. Gọi M , N lần lượt là trung điểm AK và CĐ . Biết B(1;2), N(-3;0) . Viết phương trình đường tròn ngoại tiếp tam giác BM