Các câu hỏi tương tự
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AD8,CD6,AC12. Tính diện tích toàn phần
S
t
p
của hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hình chữ nhật ABCD và A′B′C′D′. A.
S
t
p
576
π
B.
S
t
p
10
2...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AD=8,CD=6,AC'=12. Tính diện tích toàn phần S t p của hình trụ có hai đường tròn đáy là hai đường tròn ngoại tiếp hình chữ nhật ABCD và A′B′C′D′.
A. S t p = 576 π
B. S t p = 10 2 11 + 5 π
C. S t p = 26 π
D. S t p = 5 4 11 + 5 π
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có
A
B
a
,
A
A
2
a
.
Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là
9
π
2
a
3
. Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′. A.
4
a
3
B. ...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có A B = a , A A ' = 2 a . Biết thể tích hình cầu ngoại tiếp tứ diện ABCD′ là 9 π 2 a 3 . Tính thể tích V của hình chữ nhật ABCD.A′B′C′D′.
A. 4 a 3
B. 4 a 3 3
C. 2 a 3
D. 2 a 3 3
Trong không gian cho ABCD là hình chữ nhật, AB2, AD1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết
d
(
A
B
,
d
)
d
(
C
D
,
d
)
. Tính a biết rằng thể t...
Đọc tiếp
Trong không gian cho ABCD là hình chữ nhật, AB=2, AD=1. Đường thẳng d nằm trong mặt phẳng (ABCD) không có điểm chung với hình chữ nhật ABCD, song song với cạnh AB và cách AB một khoảng bằng a. Gọi V là thể tích của khối tròn xoay T, nhận được khi quay hình chữ nhật ABCD xung quanh trục d. Cho biết d ( A B , d ) < d ( C D , d ) . Tính a biết rằng thể tích khối T gấp 3 lần thể tích của khối cầu có đường kính AB.
A. a = 3
B. a = - 1 + 2
C. a = 1 2
D. a = 15 2
Cho đổ thị hàm số
y
x
+
1
x
-
1
có đổ thị như hình vẽ. Biết A, B, C, D thuộc đồ thị hàm số sao cho ABCD là hình chữ nhật có diện tích 6. Độ dài cạnh AB là A.
3
3
B.
3
C.
2
2
D.
2
Đọc tiếp
Cho đổ thị hàm số y = x + 1 x - 1 có đổ thị như hình vẽ. Biết A, B, C, D thuộc đồ thị hàm số sao cho ABCD là hình chữ nhật có diện tích 6. Độ dài cạnh AB là
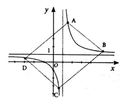
A. 3 3
B. 3
C. 2 2
D. 2
Cho hình hộp chữ nhật ABCD.A B C D có các kích thước là AB2, AD3, AA4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB A và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật. Thể tích của khối nón (N) là A.
5
π
B.
13
π
3
C.
8
π
D.
25
π
6
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A' B' C' D' có các kích thước là AB=2, AD=3, AA'=4. Gọi (N) là hình nón có đỉnh là tâm của mặt ABB' A' và đường tròn đáy là đường tròn ngoại tiếp hình chữ nhật. Thể tích của khối nón (N) là
A. 5 π
B. 13 π 3
C. 8 π
D. 25 π 6
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A′B′C′D′ và có đáy là hình tròn nội tiếp hình vuông ABCD là A.
S
xq
13
πa
2
4
B.
S
xq...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông cạnh a và cạnh bên bằng 3a. Diện tích xung quanh Sxq của hình nón có đỉnh là tâm O của hình vuông A′B′C′D′ và có đáy là hình tròn nội tiếp hình vuông ABCD là
A. S xq = 13 πa 2 4
B. S xq = 37 πa 2 12
C. S xq = 13 πa 2 12
D. S xq = 37 πa 2 4
Cho hình hộp đứng ABCD.A¢B¢C¢D¢ có AB a, AD
2
a
, BD
a
3
. Góc tạo bởi AB¢ và mặt phẳng (ABCD) bằng
60
o
.
Tính thể tích của khối chóp D¢.ABCD. A.
3
3
a
3
.
B.
3
a
2
.
C....
Đọc tiếp
Cho hình hộp đứng ABCD.A¢B¢C¢D¢ có AB = a, AD = 2 a , BD = a 3 . Góc tạo bởi AB¢ và mặt phẳng (ABCD) bằng 60 o . Tính thể tích của khối chóp D¢.ABCD.
A. 3 3 a 3 .
B. 3 a 2 .
C. a 3 .
D. 2 3 3 a 3 .
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có cạnh
AB
a
,
BC
3
a
,
A
C
26
a
.
Thể tích của khối hộp chữ nhật đó là A.
12
a
3
B.
3
a
3
C.
4
a
3...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A′B′C′D′ có cạnh AB = a , BC = 3 a , A ' C = 26 a . Thể tích của khối hộp chữ nhật đó là
A. 12 a 3
B. 3 a 3
C. 4 a 3
D. 6 a 3
Một miếng giấy hình chữ nhật ABCD với
A
B
x
,
B
C
2
x
và đường thẳng
∆
nằm trong mặt phẳng (ABCD),
∆
song song với AD và cách AD một khoảng bằng a,
∆
không có điểm chung với hình chữ nhật ABCD và khoảng cách từ A đến B đến
∆
. Tìm thể tích lớn nhất có thể có của khi quay hình chữ nhật ABCD quanh
∆
. A. ...
Đọc tiếp
Một miếng giấy hình chữ nhật ABCD với A B = x , B C = 2 x và đường thẳng ∆ nằm trong mặt phẳng (ABCD), ∆ song song với AD và cách AD một khoảng bằng a, ∆ không có điểm chung với hình chữ nhật ABCD và khoảng cách từ A đến B đến ∆ . Tìm thể tích lớn nhất có thể có của khi quay hình chữ nhật ABCD quanh ∆ .
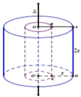
A. 64 π a 3 27 .
B. 64 π a 3 .
C. 63 π a 3 27 .
D. 64 π 27 .