Question

Cho hình chữ nhật ABCD, AB=8cm, BC=6cm

BH \(\perp\) AC tại H, DM \(\perp\) AC tại M

- CM : tam giác ABH đồng dạng với tam giác ACB từ đó suy ra AC.AH=AB²

Answer 1

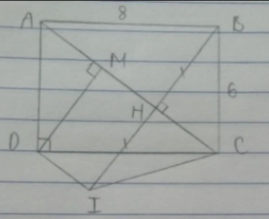
Xét ΔABH và ΔACB có:

∠BHA = ∠CBA = 90^o

∠BAH = ∠CAB (góc chung)

⇒ Hai tam giác đồng dạng

⇒ BA/CA = AB/AH

⇒ AB² = AC.AH

Answer 2

Xét ΔABH vuông tại H và ΔACB vuông tại B có 

\(\widehat{BAH}\) chung

Do đó: ΔABH\(\sim\)ΔACB

Suy ra: \(\dfrac{AB}{AC}=\dfrac{AH}{AB}\)

hay \(AB^2=AC\cdot AH\)