a) Ta có AD = BC; AD // BC (gt), AM = CN (gt)
⇒ AD – AM = BC – CN
Hay DM = BN
Lại có DM // BN
Do đó MNDN là hình bình hành ⇒ BM // DN
Cho hình chữ nhật ABCD (AB > AD). Trên cạnh AD, BC lần lượt lấy các điểm M và N sao cho AM = CN.
c) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt cạnh CD tại Q. chứng minh rằng PBQD là hình thoi.
Cho hình chữ nhật ABCD (AB > AD). Trên cạnh AD, BC lần lượt lấy các điểm M và N sao cho AM = CN.
b) Gọi O là trung điểm của BD. Chứng minh AC, BD, MN đồng quy tai O.
Cho hình chữ nhật ABCD (AB > AD). Trên cạnh AD, BC lần lượt lấy các điểm M và N sao cho AM = CN.
d) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. Chứng minh rằng: AC ⊥ CK.
Cho hình bình hành ABCD. Trên các cạnh AB và CD lần lượt lấy các điểm M và N sao cho AM = DN. Đường trung trực của BM lần lượt cắt các đường thẳng MN và BC tại E và F. a) Chứng minh tứ giác AMND là hình bình hành. b) Chứng minh rằng tứ giác MEBF là hình thoi. c) Hình bình hành ABCD phải có thêm điều kiện gì để tứ giác BCNE là hình thang cân.
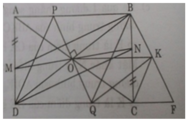
Cho hình chữ nhật ABCD (AB>AD). Trên cạnh AD,BC lần lượt lấy các điểm M, N sao cho AM=CN
A) CHỨNG MINH RẰNG BM//DN
B) Gọi O là trung điểm của BD. CHỨNG MINH AC, BD, MN đồng quy tại O
C) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt CD tại Q. CHỨNG MINH: Tứ giác PBQD là hình thoi
D) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. CHỨNG MINH: Tứ giác OBKQ là hình chữ nhật và BC _|_(vuông góc ) OK
Cho hình vuông ABCD, trên cạnh AB lấy điểm E và trên cạnh AD lấy điểm F sao cho AE = AF. Vẽ AH vuông góc với BF (H thuộc BF), AH cắt DC và BC lần lượt tại hai điểm M, N.
1. Chứng minh rằng tứ giác AEMD là hình chữ nhật.
2.CM: ∆CBH~∆EAH
3. Chứng minh rằng: \(\frac{1}{AD^2}=\frac{1}{AM^2}+\frac{1}{AN^2}\)
Cho tam giác ABC có O là trung điểm của cạnh AC. Trên tia BO lấy điểm D sao cho OD=OB.
a. Chứng minh tứ giác ABCD là hình bình hành.
b. Trên cạnh BC lấy điểm M,N sao cho BM=MN=NC. Tia NO cắt AD,AB lần lượt tại I và K. Chứng minh AI=NC và AM song song với IN.
Cho hình bình hành ABCD. Trên hai cạnh AD và CB lần lượt lấy hai điểm E và F sao cho AE = CF. Trên hai cạnh BA và DC lần lượt lấy hai điểm M và N sao cho BM = DN. Chứng minh rằng:
a) Tứ giác EMFN là hình bình hành.
b) Bốn đường thẳng AC, BD, EF, MN đồng quy.
1) Cho hình bình hành ABCD, trên cạnh AB và CD lần lượt lấy M và N sao cho AM=DN. Đừng trung trực của BM lần lượt cắt MN và BC tại E và F.
a)Chứng minh: E và F đối xứng qua AB
b)Chứng minh: MEBF là hình thoi
c)Hình bình hành ABCD cần thêm điều kiện gì để BCNE là hình thang cân
2)Cho hình bình hành ABCD, trên đường chéo AC lấy hai điểm M và N sao cho AM=CN <1/2 AC a)BNDM là hình gì?
b)BM cắt AD tại K. Xác định vị trí của M để K là trung điểm của AD
3)Cho tam giác ABC cân tại A, BM và CN là đường trung tuyến cắt nhau tại G. Gọi E,F lần lượt là trung điểm của BG và CG. Biết: EFMN là hình chữ nhật; AB=25cm; BC=14cm, tính diện tích EFMN?
