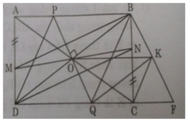
b) O là trung điểm của BD mà ABCD là hình chữ nhật nên đường chéo thứ hai AC phải qua O.
Lại có tứ giác BMDN là hình bình hành nên MN phải đi qua trung điểm O của BD.
Vậy AC, BD, MN đồng quy tại O.

b) O là trung điểm của BD mà ABCD là hình chữ nhật nên đường chéo thứ hai AC phải qua O.
Lại có tứ giác BMDN là hình bình hành nên MN phải đi qua trung điểm O của BD.
Vậy AC, BD, MN đồng quy tại O.
Cho hình chữ nhật ABCD (AB>AD). Trên cạnh AD,BC lần lượt lấy các điểm M, N sao cho AM=CN
A) CHỨNG MINH RẰNG BM//DN
B) Gọi O là trung điểm của BD. CHỨNG MINH AC, BD, MN đồng quy tại O
C) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt CD tại Q. CHỨNG MINH: Tứ giác PBQD là hình thoi
D) Đường thẳng qua B song song với PQ và đường thẳng qua Q song song với BD cắt nhau tại K. CHỨNG MINH: Tứ giác OBKQ là hình chữ nhật và BC _|_(vuông góc ) OK
Cho hình chữ nhật ABCD (AB > AD). Trên cạnh AD, BC lần lượt lấy các điểm M và N sao cho AM = CN.
c) Qua O vẽ đường thẳng d vuông góc với BD, d cắt AB tại P, cắt cạnh CD tại Q. chứng minh rằng PBQD là hình thoi.
Cho hình chữ nhật ABCD , AC cắt BD tại O . Lấy M là một điểm thuộc cạnh CD , MO cắt AB tại N
a) Chứng minh : tứ giác BNDM là hình bình hành
b) Từ điểm M , N kẻ đường thẳng song song với AC , lần lượt cắt AD và BC tại E , F . Chứng minh : MENF là hình bình hành
c) Chứng minh : 3 đường thẳng AC , MN , EF đồng quy
d) Cho BD cắt NF tại I . Chứng minh : I là trung điểm của NF
Cho hình chữ nhật ABCD , AC cắt BD tại O . Lấy M là một điểm thuộc cạnh CD , MO cắt AB tại N
a) Chứng minh : tứ giác BNDM là hình bình hành
b) Từ điểm M , N kẻ đường thẳng song song với AC , lần lượt cắt AD và BC tại E , F . Chứng minh : MÈN là hình bình hành
c) Chứng minh : 3 đường thẳng AC , MN , EF đồng quy
d) Cho BD cắt NF tại I . Chứng minh : I là trung điểm của NF
Cho hình bình hành ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Một đường thẳng đi qua O và cắt cạnh AD ở P và cạnh BC ở Q.
a. Chứng minh rằng OP = OQ.
b. Trên các cạnh AB, BC, CD, DA lấy lần lượt các điểm E, F, G, H sao cho tứ giác EFGH là hình bình hành. Chứng minh bốn đoạn AC, EG, FH và BD đồng quy.
Cho hình chữ nhật ABCD (AB<AD). Trên các cạnh
AD và BC lấn lượt lấy các điểm E và F sao cho AF = CF.
a) Chứng minh rằng: AF// CE.
b) Gọi O là giao điểm của AC và BD. Chứng minh rằng E đối xửng
với F qua O.
c) Qua C kẻ đường thẳng vuông góc với tia AF tại H. Chứng minh
răng BH vuông góc với DH
d) Biết CBH = 30°, tỉnh số đo của góc AÔH?
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm E và trên cạnh CD lấy điểm F sao cho AE = CF. Trên cạnh AD lấy điểm M và trên cạnh BC lấy điểm N sao cho AM = CN.
a) Tứ giác MENF là hình gì? Vì sao?
b) Chứng minh các đường thẳng AC;BD;EF và MN đồng quy tại 1 điểm.
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm M, trên cạnh DC lấy điểm N sao cho AM = CN.
a) Chứng minh AN//CM ;
b) Gọi O là giao điểm của AC và BD. Chứng minh O là trung điểm của MN.
Cho hình bình hành \(ABCD\) . Trên các cạnh AB và CD lấy các điểm E và F sao cho AE=CF, trên các cạnh AD và BC lấy điểm M và N sao cho AM=CN.
1)
a) Tứ giác MENF là hình gì ? Vì sao ?
b) Chứng minh các đường thẳng AC,BD,EF và MN đồng quy .
2) Nếu AE = CF = AB : 2 và AM = CN = AD : 2 thì tứ giác MENF là hình gì khi ABCD là hình thoi ? ABCD là hình chữ nhật .