Các câu hỏi tương tự
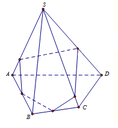
Cho hình chóp tứ giác đều S.ABCD, đuờng cao SO. Biết rằng trong các thiết diện của hình chóp cắt bởi các mặt phẳng chứa SO, thiết diện có diện tích lớn nhất là tam giác đều cạnh bằng a, tính thể tích khối chóp đã cho A.
a
3
2
6
B.
a
3
3
12
C. ...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD, đuờng cao SO. Biết rằng trong các thiết diện của hình chóp cắt bởi các mặt phẳng chứa SO, thiết diện có diện tích lớn nhất là tam giác đều cạnh bằng a, tính thể tích khối chóp đã cho
A. a 3 2 6
B. a 3 3 12
C. a 3 3 4
D. a 3 3 6
Cho hình chóp A.BCD có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A trên mặt phẳng đáy là trung điểm H của CD. Cắt hình chóp bởi mặt phẳng
(
α
)
song song với AB và CD. Tính diện tích S của thiết diện thu được, biết
d
(
B
,
(
α
)
)
a
2
,
A
B
a
2
A. ...
Đọc tiếp
Cho hình chóp A.BCD có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A trên mặt phẳng đáy là trung điểm H của CD. Cắt hình chóp bởi mặt phẳng ( α ) song song với AB và CD. Tính diện tích S của thiết diện thu được, biết d ( B , ( α ) ) = a 2 , A B = a 2
A. S = 4 a 15 ( a 15 + 2 a 2 )
B. S = 4 a 15 ( a 15 + a 2 )
C. S = 4 a 15 ( a 15 - 2 a 2 )
D. S = 4 a 15 ( a 15 - a 2 )
Cho tứ diện ABCD và M, N là các điểm thay đổi trên cạnh AB và CD sao cho
A
M
M
B
C
N
N
D
. Gọi P là một điểm trên cạnh AC và S là diện tích thiết diện cắt bởi mặt phẳng
M
N
P
và hình chóp. Tính tỉ số k của diện tích tam giác MNP và diện tích thiết diện S. A....
Đọc tiếp
Cho tứ diện ABCD và M, N là các điểm thay đổi trên cạnh AB và CD sao cho A M M B = C N N D . Gọi P là một điểm trên cạnh AC và S là diện tích thiết diện cắt bởi mặt phẳng M N P và hình chóp. Tính tỉ số k của diện tích tam giác MNP và diện tích thiết diện S.
A. 2 k k + 1 .
B. 1 k .
C. k k + 1 .
D. 1 k + 1 .
Cho hình chóp S.ABCD có đáy là hình thang ABCD,AB//CD, AB2AD. M là một điểm thuộc cạnh AD,
α
là mặt phẳng qua M và song song với mặt phẳng (SAB). Biết diện tích thiết diện của hình chóp cắt bởi mặt phẳng
α
bằng
2
3
diện tích tam giác SAB. Tính tỉ số
k
M
A
M
D
.
A....
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang ABCD,AB//CD, AB=2AD. M là một điểm thuộc cạnh AD, α là mặt phẳng qua M và song song với mặt phẳng (SAB). Biết diện tích thiết diện của hình chóp cắt bởi mặt phẳng α bằng 2 3 diện tích tam giác SAB. Tính tỉ số k = M A M D .
A. k = 1 2
B. k = 1
C. k = 3 2
D. k = 2 3
Cho hình chóp A.BCD có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A trên mặt phẳng đáy là trung điểm H của CD. Cắt hình chóp bởi mặt phẳng
α
song song với AB và CD. Tính diện tích S của thiết diện thu được, biết
d
B
;
α
a
2
v
à
A
B
a
2...
Đọc tiếp
Cho hình chóp A.BCD có đáy là tam giác đều cạnh a. Hình chiếu vuông góc của A trên mặt phẳng đáy là trung điểm H của CD. Cắt hình chóp bởi mặt phẳng α song song với AB và CD. Tính diện tích S của thiết diện thu được, biết d B ; α = a 2 v à A B = a 2
A. S = 4 a 15 a 15 + 2 a 2
B. S = 4 a 15 a 15 - a 2
C. S = 4 a 15 a 15 - 2 a 2
D. S = 4 a 15 a 15 + a 2
Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng a. Người ta cắt khối đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. (Giả thiết rằng tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá ban đầu). A.
2
a
2
3...
Đọc tiếp
Một viên đá có hình dạng là khối chóp tứ giác đều với tất cả các cạnh bằng a. Người ta cắt khối đá đó bởi mặt phẳng song song với đáy của khối chóp để chia khối đá thành hai phần có thể tích bằng nhau. Tính diện tích của thiết diện khối đá bị cắt bởi mặt phẳng nói trên. (Giả thiết rằng tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá ban đầu).
A. 2 a 2 3
B. a 2 2 3
C. a 2 4
D. a 2 4 3
Cho hình chóp tứ giác
S
.
A
B
C
D
có thể tích bằng V. Lấy điểm A’ trên cạnh SA sao cho
S
A
1
3
S
A
. Một mặt phẳng qua A’ và song song với đáy của hình chóp cắt các cạnh
S
B
,
S
C
,
S
D
lần lượt tại
B
,
C
,
D...
Đọc tiếp
Cho hình chóp tứ giác S . A B C D có thể tích bằng V. Lấy điểm A’ trên cạnh SA sao cho S A ' = 1 3 S A . Một mặt phẳng qua A’ và song song với đáy của hình chóp cắt các cạnh S B , S C , S D lần lượt tại B ' , C ' , D ' . Khi đó thể tích của khối chóp S . A ' B ' C ' D ' tính theo a bằng
A. V 3
B. V 9
C. V 27
D. V 81
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
AB
a
,
BC
a
2
,
SA
a
3
và SA vuông góc với mặt phẳng (ABC). Biết (P) là mặt phẳng qua A và vuông góc với SB. Diện tích thiết diện cắt bởi (P) và hình chóp là A.
S
a
2
6...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB = a , BC = a 2 , SA = a 3 và SA vuông góc với mặt phẳng (ABC). Biết (P) là mặt phẳng qua A và vuông góc với SB. Diện tích thiết diện cắt bởi (P) và hình chóp là
A. S = a 2 6 8
B. S = 3 a 2 6 16
C. S = a 2 6 16
D. S = a 2 30 8
Cho khối chóp S.ABCD có đáy là hình bình hành, gọi B và D theo thứ tự là trung điểm các cạnh SB, SD. Mặt phẳng (ABD)cắt cạnh SC tại C’. Tính tỷ số thể tích của hai khối đa diện được chia ra bởi mặt phẳng (ABD). A.
1
2
B.
1
6
C.
1
12
D.
1
5
Đọc tiếp
Cho khối chóp S.ABCD có đáy là hình bình hành, gọi B' và D' theo thứ tự là trung điểm các cạnh SB, SD. Mặt phẳng (AB'D')cắt cạnh SC tại C’. Tính tỷ số thể tích của hai khối đa diện được chia ra bởi mặt phẳng (AB'D').
A. 1 2
B. 1 6
C. 1 12
D. 1 5