Đáp án A
Gọi O là tâm hình vuông ABCD và M là trung điểm CD có S O = a 2 2 và H là hình chiếu vuông góc của G lên mặt phẳng (ABCD).
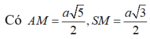
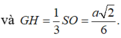
Vì
![]()
![]()
![]()
Và
![]()
![]()
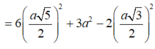
![]()
Vì vậy
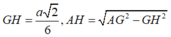
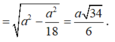
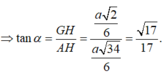
Đáp án A
Gọi O là tâm hình vuông ABCD và M là trung điểm CD có S O = a 2 2 và H là hình chiếu vuông góc của G lên mặt phẳng (ABCD).
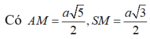
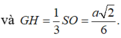
Vì
![]()
![]()
![]()
Và
![]()
![]()
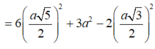
![]()
Vì vậy
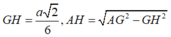
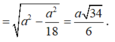
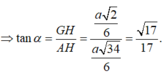
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng
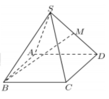
A. 2 2
B. 3 2
C. 2 3
D. 1 3
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng:
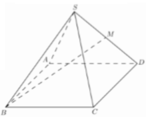
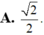

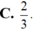
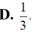
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a (tham khảo hình vẽ bên). Côsin góc giữa hai mặt phẳng (SCD) và (ABCD) bằng
A. 3 3
B. 1 2
C. 3 2
D. 3 6
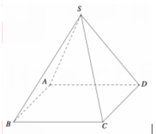
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 6a. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trọng tâm G của tam giác ABD d(G,(SAD))=a (tham khảo hình vẽ bên). Tính khoảng cách giữa hai đường thẳng SD và BC.
A. 2a
B. 3a
C. 4a
D. 3 a 2
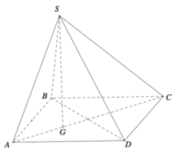
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng nhau. Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng BM và AD bằng
A. 3 5 10
B. 3 5 20
C. 55 10
D. 155 20
Cho hình chóp tứ giác đều S.ABCD có tất cả cạnh bằng a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng SA và CD bằng
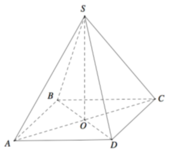
A. a 6 6
B. a 3 3
C. a 3 6
D. a 6 3
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là điểm trên đoạn SD sao cho SM=2MD.
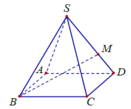
Tan góc giữa đường thẳng BM và mặt phẳng (ABCD) là
A. 1 3
B. 5 5
C. 3 3
D. 1 5
Cho hình chóp đều tứ giác đều S ABCD . có tất cả các cạnh bằng a . Gọi O là giao điểm AC và BD
a) Chứng minh SA vuông góc với SC.
b) Tính góc giữa mặt bên và mặt đáy.
c) Tính khoảng cách từ A đến mặt phẳng (SCD)
Cho tứ diện đều ABCD. Gọi M là trung điểm cạnh AC (tham khảo hình vẽ bên). Tang góc giữa đường thẳng BM và mặt phẳng (BCD) bằng
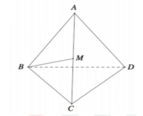
A. 3 6
B. 2 3
C. 14 7
D. 14 2