Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hình chiếu của S lên đáy ABCD trùng với trọng tâm tam giác ABD. Mặt bên (SAB) tạo với đáy góc 60 ο . Tính theo a khoảng cách từ B đến mặt phẳng (SAD)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh bên SA vuông góc với đáy và SC tạo với (SAD) góc 30 o . Gọi G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SCD).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của AB, tam giác SAB vuông cân tại S. Biết SH a, CH
a
3
. Tính khoảng cách giữa hai đường thẳng SD và CH
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là trung điểm H của AB, tam giác SAB vuông cân tại S. Biết SH = a, CH= a 3 . Tính khoảng cách giữa hai đường thẳng SD và CH
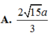
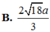
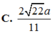
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh A. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm I thuộc đoạn AB sao cho BI 2AI. Góc giữa mặt bên (SCD) và mặt đáy (ABCD) bằng
60
0
. Tính khoảng cách giữa hai đường thẳng AD và SC.
A
.
93
31
a
B
.
3
93...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh A. Hình chiếu vuông góc của S lên mặt phẳng (ABCD) là điểm I thuộc đoạn AB sao cho BI = 2AI. Góc giữa mặt bên (SCD) và mặt đáy (ABCD) bằng 60 0 . Tính khoảng cách giữa hai đường thẳng AD và SC.
A . 93 31 a
B . 3 93 31 a
C . 93 31
D . 3 93 31 a
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, AB = 2a, B D = A C 3 , mặt bên SAB là tam giác cân đỉnh A, hình chiếu vuông góc của đỉnh S trên mặt phẳng đáy trùng với trung điểm H của AI. Khoảng cách giữa hai đường thẳng SB và CD bằng bao nhiêu?
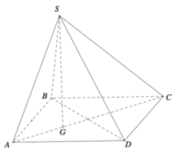
Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Gọi G là trọng tâm của tam giác đáy ABC.
a) Tính khoảng cách từ S tới mặt phẳng đáy (ABC).
b) Tính khoảng cách giữa hai đường thẳng AB và SG.
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên SC
a
15
Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng
2
a
6
Tính thể tích V của khối chóp S.ABCD?
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên SC= a 15 Tam giác SAD là tam giác đều cạnh bằng 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm AD, khoảng cách từ B đến mặt phẳng (SHC) bằng 2 a 6 Tính thể tích V của khối chóp S.ABCD?
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên SC
a
15
Tam giác SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm của cạnh AD, khoảng cách từ B tới mặt phẳng (SHC) bằng
2
6
a
Tính thể tích V của khối chóp S.ABCD?
Đọc tiếp
Cho hình chóp S.ABCD với đáy ABCD là hình thang vuông tại A và D, đáy nhỏ của hình thang là CD, cạnh bên SC= a 15 Tam giác SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góc với đáy. Gọi H là trung điểm của cạnh AD, khoảng cách từ B tới mặt phẳng (SHC) bằng 2 6 a Tính thể tích V của khối chóp S.ABCD?
![]()
![]()
![]()
![]()
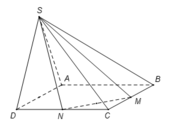
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung điểm của BC và CD (tham khảo hình vẽ bên). Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.CMN A.
R
a
37
6
B.
R...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M và N lần lượt là trung điểm của BC và CD (tham khảo hình vẽ bên). Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.CMN
A. R = a 37 6
B. R = a 29 8
C. R = 5 a 3 12
D. R = a 93 12